DP

Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.

In both contexts it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have optimal substructure.

If sub-problems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the sub-problems.[1] In the optimization literature this relationship is called the Bellman equation.

Situation

Optimal substructure properties If the solution of the sub-problem included in the optimal solution of the problem is also optimal, we say that the problem has the optimal sub-structure properties (that is, the principle of optimization is satisfied). The optimal substructure properties provide important clues for dynamic programming algorithms to solve problems.
No aftereffects That is, once the solution of the sub-problem is determined, it will not change, and it will not be affected by the decision-making of the larger problem that contains it after that.
Sub-problem overlapping The sub-problem overlap property means that when recursive algorithm is used to solve the problem from top to bottom, the sub-problem generated each time is not always a new problem, and some sub-problems will be calculated repeatedly. The dynamic programming algorithm makes use of the overlapping nature of such sub-problems. It calculates each sub-problem only once, and then saves its calculation results in a table. When it is necessary to calculate the sub-problems that have been calculated again, it is only in the table Simply look at the results to obtain higher efficiency.

Longest-palindromic-substring

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.
Example 2:

Input: "cbbd"
Output: "bb"

My Github Code and Thinking

Consider whether there are repetitive sub-problems Yes, every time it is necessary to judge whether its substring is a palindromic string
Define the status Use a two-dimensional array to store state, where
dp [i] [j] means s [i, j] Initialize a two-dimensional array with each item of NxN equal to 1, where dp [0] [0] means that if the input string is empty, it must be a palindrome string
State transition expressions

dp[i][j] = dp[i-1][j+1] if s[i] == s[j] else 0

Update the longest palindromic string

if dp[i][j]:
	c = i-j+1
	if c > end:
		begin = j
		end = c

动态规划

通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。

动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。

通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

适用情况

最优子结构性质 如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
无后效性 即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
子问题重叠性质 子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

思考步骤

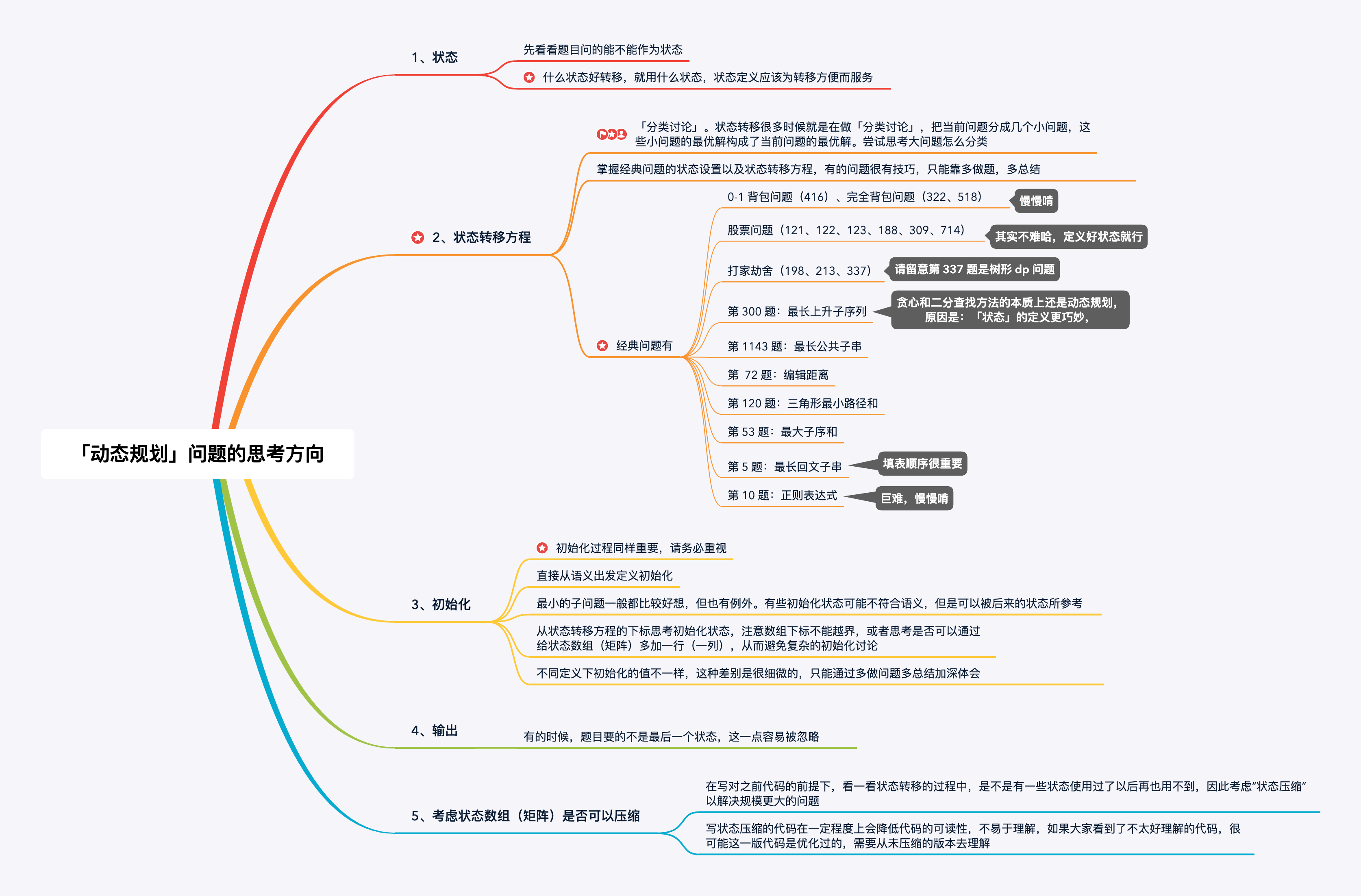
引用自liweiwei

以最长回文字符串举例

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2：

输入: "cbbd"
输出: "bb"

源码

思考是否有重复子问题是的,每次都要判断它的子字符串是否是回文字符串
定义状态使用二维数组存储状态,其中 dp[i][j] 表示s[i, j] 初始化一个NxN的每一项等于1的二维数组,其中 dp[0][0]表示如果输入字符串为空则一定为回文串
状态转移方程

上一个状态到下一个状态之间的关系即状态是如何转移的

dp[i][j] = dp[i-1][j+1] if s[i] == s[j] else 0

更新最长回文字符串

if dp[i][j]:
	c = i-j+1
	if c > end:
		begin = j
		end = c