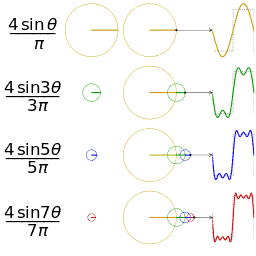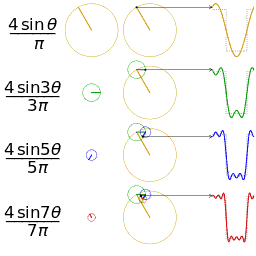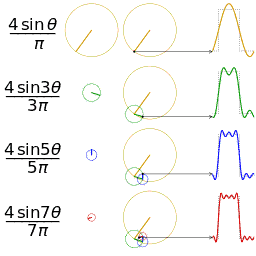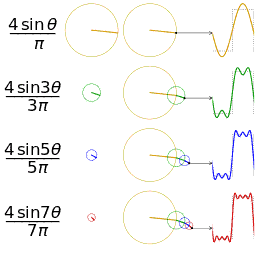Fourier Series
| EN | CN |
Definition
Formula
\begin{equation} \begin{split} f(t)&=\frac{a_{0}}{2}+a_{1}cos(\omega t)+b_{1}sin(\omega t) \ &+a_{2}cos(2\omega t)+b_{2}sin(2\omega t) \ &+…\ &=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}{[a_{n}cos(n\omega t)+b_{n}sin(n\omega t)]} \end{split} \end{equation}
And the an ,bn
\begin{aligned} a_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)cos(n\omega t)dt \ b_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)sin(n\omega t)dt \end{aligned}
傅里叶级数
定义
在数学中,傅里叶级数(Fourier series,/ˈfʊrieɪ, -iər/)是把类似波的函数表示成简单正弦波的方式。更正式地说,它能将任何周期函数或周期信号分解成一个(可能由无穷个元素组成的)简单振荡函数的集合,即正弦函数和余弦函数(或者,等价地使用复指数)。离散时间傅里叶变换是一个周期函数,通常用定义傅里叶级数的项进行定义
公式