FSM
| EN | CN |
A finite-state machine (FSM) or finite-state automaton (FSA, plural: automata), finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition.An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines.A deterministic finite-state machine can be constructed equivalent to any non-deterministic one.
The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions depending on a sequence of events with which they are presented. Simple examples are vending machines, which dispense products when the proper combination of coins is deposited, elevators, whose sequence of stops is determined by the floors requested by riders, traffic lights, which change sequence when cars are waiting, and combination locks, which require the input of a sequence of numbers in the proper order.
The finite-state machine has less computational power than some other models of computation such as the Turing machine.The computational power distinction means there are computational tasks that a Turing machine can do but a FSM cannot. This is because a FSM’s memory is limited by the number of states it has. FSMs are studied in the more general field of automata theory.
Example
65 Valid Number
Validate if a given string can be interpreted as a decimal number.
Some examples:
"0" => true
" 0.1 " => true
"abc" => false
"1 a" => false
"2e10" => true
" -90e3 " => true
" 1e" => false
"e3" => false
" 6e-1" => true
" 99e2.5 " => false
"53.5e93" => true
" --6 " => false
"-+3" => false
"95a54e53" => false
Note: It is intended for the problem statement to be ambiguous. You should gather all requirements up front before implementing one. However, here is a list of characters that can be in a valid decimal number:
Numbers 0-9
Exponent - "e"
Positive/negative sign - "+"/"-"
Decimal point - "."
Of course, the context of these characters also matters in the input.

- 有限状态机
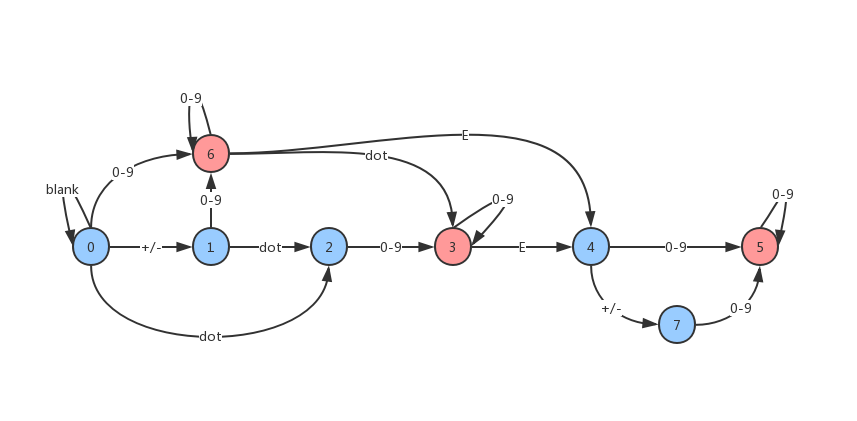
The constructed state machine is shown in the cover picture (red is the termination state and blue is the intermediate state). According to the explanation of “Compiling Principles”, DFA accepts the string s as input from state 0. When s is exhausted, if the current state is in an intermediate state, it is rejected; if it reaches the termination state, it is accepted.
class Solution():
'''有限状态机FSM'''
def __init__(self):
self.state = [x for x in range(9)]
def state(self):
return self.state
def isNumber(self, s):
"""
:type s: str
:rtype: bool
一. 为什么会有9种状态
-1 其它直接退出的状态
0 blank
1 +/-
2 dot
3 Decimal places
4 E
5 Number of digits after E
6 Number
7 +/- in the right of E
8 the blank to the right of number
二. Special number
'1.' equal to 1.0
'+.9e8'or'-.9e8' is number
"""
b = ' '# 32
positive_sign = '+'#43
nagtive_sign = '-'#45
number = '9'
is_numbers = [chr(i) for i in range(48,58)]
dot = '.'#46
E = 'e'#101
other = '-1'
others = [32,43,45,46,101]
dfa = { b: [0,-1,-1,8,-1,8,8,-1,8],
positive_sign:[1,-1,-1,-1,7,-1,-1,-1,-1],
nagtive_sign: [1,-1,-1,-1,7,-1,-1,-1,-1],
number: [6,6,3,3,5,5,6,5,-1],
dot: [2,2,-1,-1,-1,-1,3,-1,-1],
E: [-1,-1,-1,4,-1,-1,4,-1,-1],
other: [-1,-1,-1,-1,-1,-1,-1,-1,-1]
}
start = self.state[0]
#print dfa
for i in s:
if i in is_numbers:
i = number
if ord(i) not in range(48,58):
if ord(i) not in others:
i = other
start = dfa[i][start]
#print i,start
if start == -1:
return False
if start == 3 or start == 6 or start == 8 or start == 5:
return True
else:
return False
- float()
Syntactic sugar of python by using Python’s coercion type float()

class Solution(object):
def isNumber(self, s):
"""
:type s: str
:rtype: bool
"""
try:
float(s)
return True
except Exception as e:
#print(str(e))
return False
有限状态机
有限状态机(英语:finite-state machine,缩写:FSM)又称有限状态自动机(英语:finite-state automation,缩写:FSA),简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学计算模型。我们现在使用的计算机可以说是非常普遍的一个FSM
案例
65 有效数字
验证给定的字符串是否可以解释为十进制数字。
例如:
"0" => true
" 0.1 " => true
"abc" => false
"1 a" => false
"2e10" => true
" -90e3 " => true
" 1e" => false
"e3" => false
" 6e-1" => true
" 99e2.5 " => false
"53.5e93" => true
" --6 " => false
"-+3" => false
"95a54e53" => false
说明: 我们有意将问题陈述地比较模糊。在实现代码之前,你应当事先思考所有可能的情况。这里给出一份可能存在于有效十进制数字中的字符列表:
数字 0-9
指数 - "e"
正/负号 - "+"/"-"
小数点 - "."
当然,在输入中,这些字符的上下文也很重要。

- 有限状态机
构建出来的状态机如封面图片所示(红色为 终止状态,蓝色为 中间状态)。根据《编译原理》的解释,DFA 从状态 0 接受串 s 作为输入。当s耗尽的时候如果当前状态处于中间状态,则拒绝;如果到达终止状态,则接受。
然后,根据 DFA 列出如下的状态跳转表,之后我们就可以采用 表驱动法 进行编程实现了。需要注意的是,状态 8,是用于处理串后面的若干个多余空格的。状态-1,是表示遇到了一些意外的字符,可以直接停止后续的计算。状态跳转表如下:

class Solution():
'''有限状态机FSM'''
def __init__(self):
self.state = [x for x in range(9)]
def state(self):
return self.state
def isNumber(self, s):
"""
:type s: str
:rtype: bool
一. 为什么会有9种状态
-1 其它直接退出的状态
0 空格
1 +/-
2 小数点
3 小数位
4 E
5 E后位的数
6 数字
7 科学计数法E后的+/-
8 代表末位的空格
二. 特别的数字
'1.' 等于 1.0
'+.9e8'或者'-.9e8'也是数字
"""
b = ' '# 32
positive_symbol = '+'#43
nagtive_symbol = '-'#45
number = '9'
is_numbers = [chr(i) for i in range(48,58)]
dot = '.'#46
E = 'e'#101
other = '-1'
others = [32,43,45,46,101]
dfa = { b: [0,-1,-1,8,-1,8,8,-1,8],
positive_symbol:[1,-1,-1,-1,7,-1,-1,-1,-1],
nagtive_symbol: [1,-1,-1,-1,7,-1,-1,-1,-1],
number: [6,6,3,3,5,5,6,5,-1],
dot: [2,2,-1,-1,-1,-1,3,-1,-1],
E: [-1,-1,-1,4,-1,-1,4,-1,-1],
other: [-1,-1,-1,-1,-1,-1,-1,-1,-1]
}
start = self.state[0]
#print dfa
for i in s:
if i in is_numbers:
i = number
if ord(i) not in range(48,58):
if ord(i) not in others:
i = other
start = dfa[i][start]
#print i,start
if start == -1:
return False
if start == 3 or start == 6 or start == 8 or start == 5:
return True
else:
return False
- 取巧
利用python的强制转换类型的语法糖

class Solution(object):
def isNumber(self, s):
"""
:type s: str
:rtype: bool
"""
try:
float(s)
return True
except Exception as e:
#print(str(e))
return False