Convolutional Neural Networks

Posted on | 0 comments
Words count in article 1295 | Reading time 6

Gradient Based Learning Applied to Document Recognition

定义

卷积神经网络是由输入层、卷积层、正则化层、池化层、全连阶层、输出层组成 例如LeNet,AlexNet LeNet-5

卷积层

卷积层是一个卷积核(Kernel)和输入的一个张量tensor进行卷积然后传递给激活函数计算后传递下一层

  • 张量: numberxhxwxC, 张量数量x张量长x张量宽x张量通道数
  • 卷积核的定义: 有一个通常是3x3或者5x5(一般是奇数)大小的二维张量
  • 卷积计算: 点乘的推广和延伸 \(Y[i,j] = \sum_{m=0}^{k_h-1} \sum_{n=0}^{k_w-1} W[m,n]\dot{X[i+m,j+n]} + b\)
    • \(k_h\)和\(k_w\): 卷积核的高和宽
    • W:卷积核权重矩阵
    • b:偏置项(Bias)
    • i,j:输出特征图(feature map)的位置索引
  • 激活函数: 主要作用为增加非线性能力,提高模型的robustness

卷积操作有哪些

  1. 普通卷积（Standard Convolution）
  2. 深度可分离卷积（Depthwise Separable Convolution）
  3. 转置卷积（Transpose Convolution / Deconvolution）
  4. 空洞卷积（Dilated Convolution）

解决什么问题

一开始是由Yann LeCun提出来解决邮编中数字识别问题的,再然后进行了扩展,已经应用到了现代机器学习的很多重要的领域

  1. 高维数据的处理问题
  2. 局部特征提取问题
  3. 平移不变性问题
  4. 特征自动学习问题
  5. 过拟合问题
  6. 计算效率问题
  7. 空间结构利用问题
  8. 图像分类和物体识别的精度问题

作者简介

Yann LeCun

  • 出生日期：1960年7月8日
  • 出生地点：法国
  • 国籍：法裔美国人
  • 教育背景：
    • 本科和硕士学位：巴黎第六大学（Pierre and Marie Curie University）
    • 博士学位：在巴黎第六大学获得计算机科学博士学位，专注于神经网络的学习算法.

主要贡献:

  1. 卷积神经网络（CNN）：

LeCun是卷积神经网络的主要发明者之一，特别是在20世纪80年代末，他提出了LeNet，一个用于手写数字识别的卷积神经网络。这一贡献奠定了现代计算机视觉的基础。 LeNet 是一种深度神经网络，通过卷积操作自动提取图像特征，从而在手写数字识别任务上取得了突破性的成果。

  1. 反向传播算法和优化技术：

在LeCun的研究中，他对反向传播（backpropagation）算法的应用做出了重要贡献，尤其是在深度神经网络中的有效实现。 LeCun也参与了多种优化算法的研究，推动了深度学习模型的训练效率。

  1. 深度学习和人工智能的普及：

Yann LeCun在推动深度学习和人工智能普及方面做出了巨大贡献。他的研究不仅在学术界产生了深远的影响，还在工业界（特别是计算机视觉、自动驾驶、语音识别等领域）得到了广泛应用。

优点

CNN能够自动提取特征，减少了手动设计特征的复杂性；共享参数减少了计算和存储的开销；局部感知和卷积操作使得它在图像处理和视觉任务中非常有效。

缺点

CNN对数据的要求较高，需要大量标注数据进行训练，且计算资源需求大；它对图像的旋转、尺度等变化不敏感；此外，模型的解释性差，可能存在过拟合风险。

数据集

THE MNIST DATABASE of handwritten digits

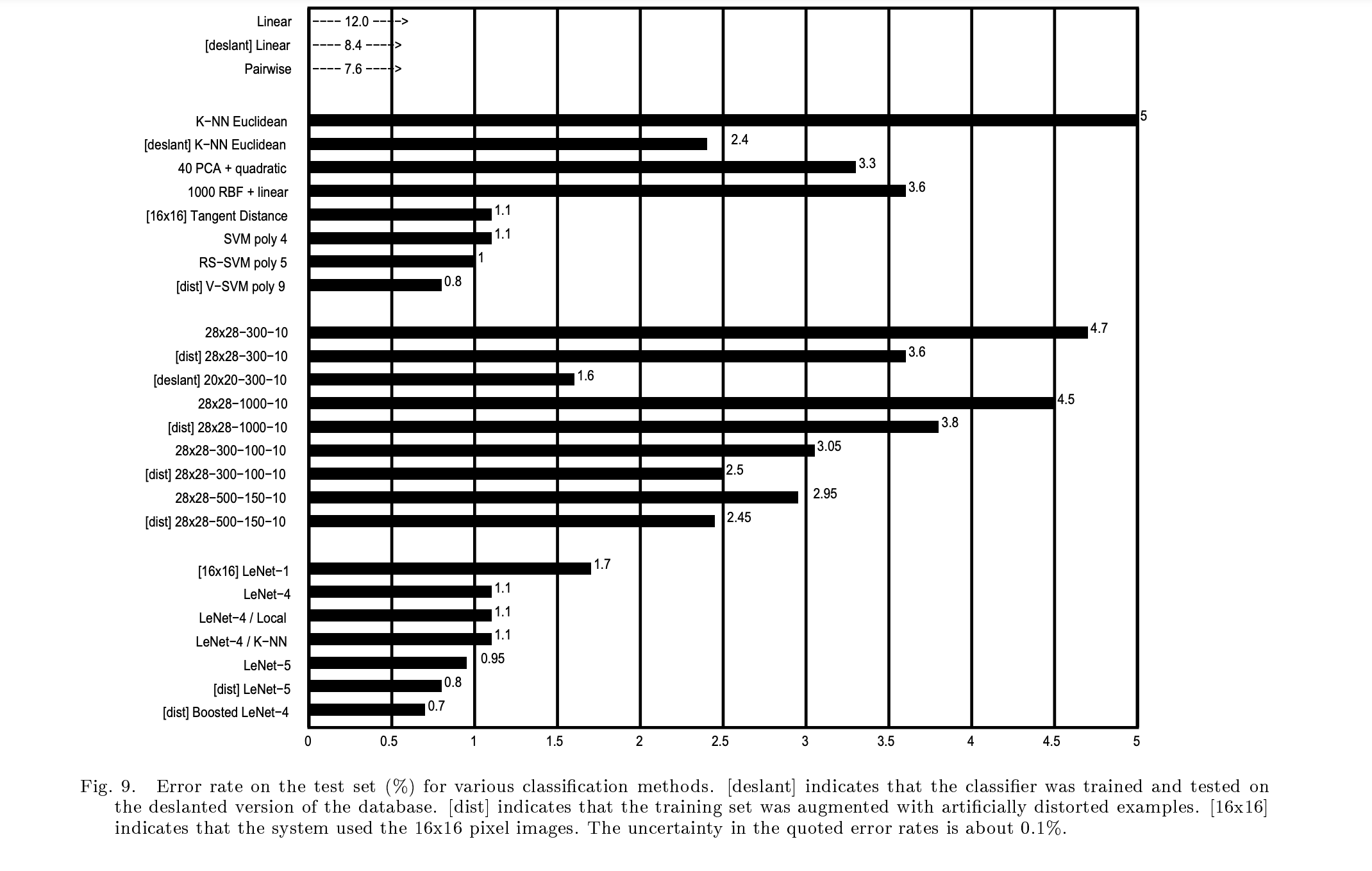
效果

[dist] Boosted LeNet-4以0.1%的优势胜于[dist] V−SVM poly 9 每种分类方法在测试集中的错误率对比

Code精读

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms

Class RBFLayer(nn.Module):
	#$$\phi (x, c) = exp(-\frac{\left \| x-c \right \| ^2}{2\sigma^2}) $$
	def __init__(self, in_features, out_features, sigma = 1.0):
		super(RBFLayer, self).__init__()
		self.centers = nn.Parameter(torch.randn(out_features, in_features))#随机初始化类别中心,需要随梯度更新每个中心的参数，距离越小，样本和类别中心之间的相似度越高。
		self.sigma = sigma #控制响应范围
	def forward(self, x):
		distance = torch.cdist(x, self.centers)# 计算输入点与中心点的距离
		return torch.exp(-distance**2/(2*self.sigma**2))

# 定义LeNet-5模型
class LeNet5(nn.Module):
    def __init__(self):
        super(LeNet5, self).__init__()
        
        # 卷积层 1： 输入通道 1 (灰度图)，输出通道 6，卷积核大小 5x5
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        self.sigmoid1 = nn.Sigmoid()
        self.pool1 = nn.AvgPool2d(kernel_size=2, stride=2)

        # 卷积层 2： 输入通道 6，输出通道 16，卷积核大小 5x5
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
        self.sigmoid2 = nn.Sigmoid()
        self.pool2 = nn.AvgPool2d(kernel_size=2, stride=2)
        
        # 卷积层 3： 输入通道 16，输出通道 120，卷积核大小 5x5
        self.conv3 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5)
        self.sigmoid3 = nn.Sigmoid()

        # 全连接层 1： 输入为 120，输出为 84
        self.fc1 = nn.Linear(120, 84)
        self.sigmoid_fc1 = nn.Sigmoid()

        # RBF 层作为输出层： 输入为 84，输出为 10（MNIST 类别数）
        self.rbf_layer = RBFLayer(in_features=84, out_features=10, sigma=1.0)

    def forward(self, x):
        # 前向传播
        x = self.pool1(self.sigmoid1(self.conv1(x)))
        x = self.pool2(self.sigmoid2(self.conv2(x)))
        x = self.sigmoid3(self.conv3(x))
        x = x.view(-1, 120)  # Flatten: 120个特征，展平为一维
        x = self.sigmoid_fc1(self.fc1(x))
        x = self.rbf_layer(x)
        return x

# 数据预处理
transform = transforms.Compose([
    transforms.ToTensor(),  # 将图像转化为Tensor
    transforms.Normalize((0.5,), (0.5,))  # 归一化,把数据范围归一化到[0,1]
])

# 加载MNIST数据集,不存在便下载
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
# 训练epoch 为64批次,且打乱数据顺序
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)

# 创建模型
model = LeNet5()

# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()  # 交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)#SGD随机梯度下降+动量

# 训练模型
epochs = 5
for epoch in range(epochs):
    model.train()
    running_loss = 0.0
    correct = 0
    total = 0
    for inputs, labels in train_loader:
        optimizer.zero_grad()# 清除上一批次梯度
        
        # 前向传播
        outputs = model(inputs)
        
        # 计算损失
        loss = criterion(outputs, labels)
        
        # 反向传播
        loss.backward()
        optimizer.step()

        # 统计
        running_loss += loss.item()# 累加每批次的损失
        _, predicted = torch.max(outputs, 1)# 获取最大概率的标签
        total += labels.size(0)
        correct += (predicted == labels).sum().item()# 获取正确数量

    epoch_loss = running_loss / len(train_loader)
    epoch_acc = 100 * correct / total # 准确率
    print(f"Epoch [{epoch+1}/{epochs}], Loss: {epoch_loss:.4f}, Accuracy: {epoch_acc:.2f}%")

# 测试模型
model.eval()  # 设置为评估模式
correct = 0
total = 0
with torch.no_grad():  # 禁用梯度计算，节省内存
    for inputs, labels in test_loader:
        outputs = model(inputs)
        _, predicted = torch.max(outputs, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

test_acc = 100 * correct / total
print(f"Test Accuracy: {test_acc:.2f}%")

参考

CS231n: Convolutional Neural Networks for Visual Recognition — Andrej Karpathy’s Stanford computer science course on CNNs in computer vision