作者简介
长短期记忆网络(Long Short-Term Memory, LSTM)由德国计算机科学家 Jürgen Schmidhuber 和他的学生 Sepp Hochreiter 于 1997 年共同提出。
- Jürgen Schmidhuber:
- Jürgen Schmidhuber 是人工智能和深度学习领域的先驱,尤其以其在递归神经网络(RNN)和 LSTM 方面的贡献而闻名。
- 他在 1990 年代初期的研究为现代深度学习奠定了基础,包括 LSTM、元学习、注意力机制和强化学习等。
- Schmidhuber 教授在其职业生涯中发表了大量关于人工智能的论文,并在多个国际会议上担任主席或委员会成员。
- Sepp Hochreiter:
- Sepp Hochreiter 是奥地利 Linz 大学的教授,现任 Linz 人工智能实验室主任。
- 他在深度学习和机器学习领域有着广泛的研究,特别是在 LSTM 和序列学习方面的贡献。
- Hochreiter 教授的研究涵盖了生物信息学、神经网络和统计学习等多个领域。
解决什么问题
LSTM 的提出解决了传统 RNN 在处理长序列时的梯度消失和梯度爆炸问题,使得神经网络能够更有效地捕捉序列数据中的长距离依赖关系。
传统RNN为什么会出现梯度消失或梯度爆炸
以下讨论的是Elman的RNN结构
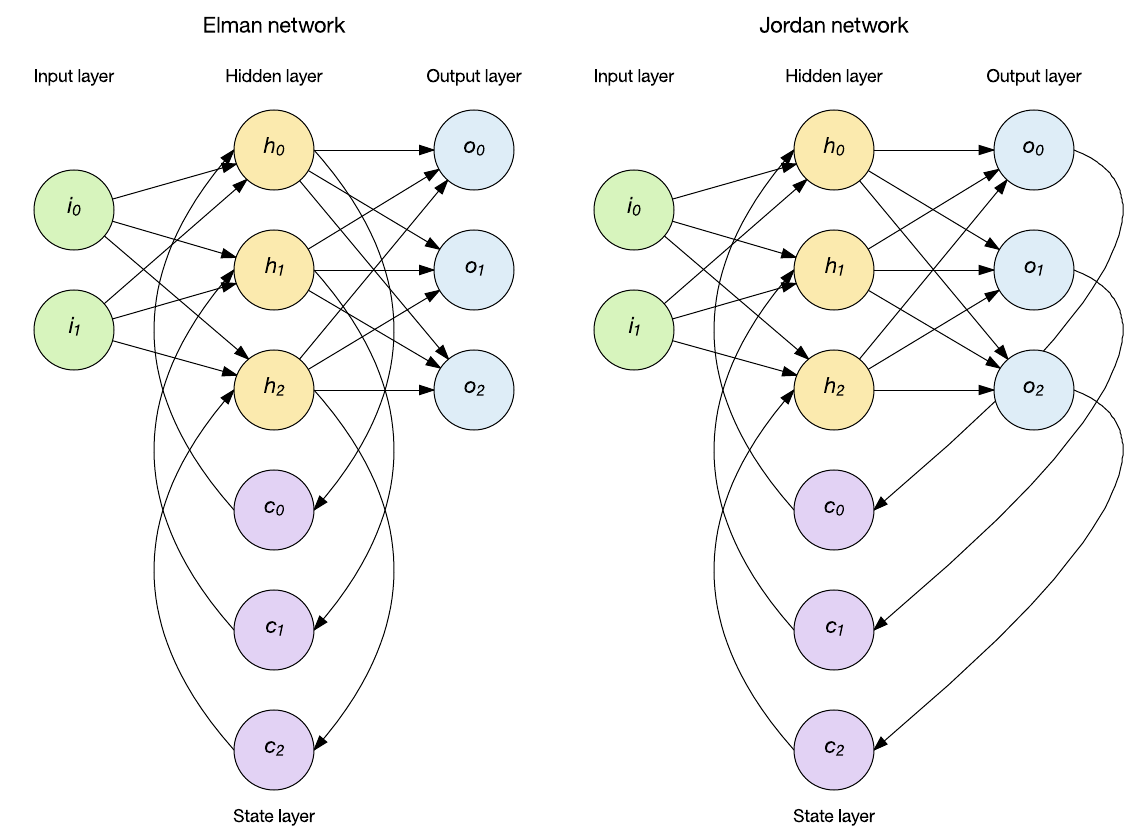 其中公式,
\(h_t = \sigma(W_tx_t + W_hh_{t-1} + b_h)\)
其中公式,
\(h_t = \sigma(W_tx_t + W_hh_{t-1} + b_h)\)
其中,
- \(W_{h}\):\(\in{R}^{n_h \times n_h}\)
- \(\frac{\partial L}{\partial z_t}\):\(\in{R}^{n_h \times 1}\)
- \(\text{diag}(\sigma'(z_t))\):\(\text{diag}(\sigma'(z_t)) = \begin{pmatrix} \sigma'(z_{t, 1}) & 0 & \cdots & 0 \\ 0 & \sigma'(z_{t, 2}) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma'(z_{t, n_h}) \end{pmatrix}_{n_h \times n_h}\)
- \(h_{t-1}^\top\):\(\in{R}^{1 \times n_h}\)
- \(\frac{\partial L}{\partial W_{h}}\):\(\in{R}^{n_h \times n_h}\)
乘积项 \((\prod_{k=T}^{t+1} \mathrm{diag}(1 - \tanh^2(z_k)) W_h)\) 的范数(如谱范数)决定了梯度的大小:
- 如果每个时间步的 \((\| \mathrm{diag}(1 - \tanh^2(z_k)) W_h \| < 1)\),则梯度消失。
- 如果 \((\| \mathrm{diag}(1 - \tanh^2(z_k)) W_h \| > 1)\),则梯度爆炸。
优缺点
| 优点 | 缺点 |
|---|---|
| 解决梯度消失问题 LSTM 通过引入门控机制,有效缓解了传统 RNN 在处理长序列时的梯度消失问题。 |
计算复杂度高 由于引入了门控机制和长期记忆机制,LSTM 的计算复杂度较高,训练时间较长。 |
| 捕捉长期依赖关系 LSTM 能够更好地捕捉序列数据中的长期依赖关系,在处理长序列数据时表现出色。 |
难以解释 LSTM 的模型结构较为复杂,不易理解和调试。 |
| 适用于多种类型的输入 LSTM 可以处理多种类型的输入,如文本、音频和图像等。 |
对输入序列长度敏感 LSTM 对于输入序列的长度敏感,需要对序列进行截断或填充。 |
实验
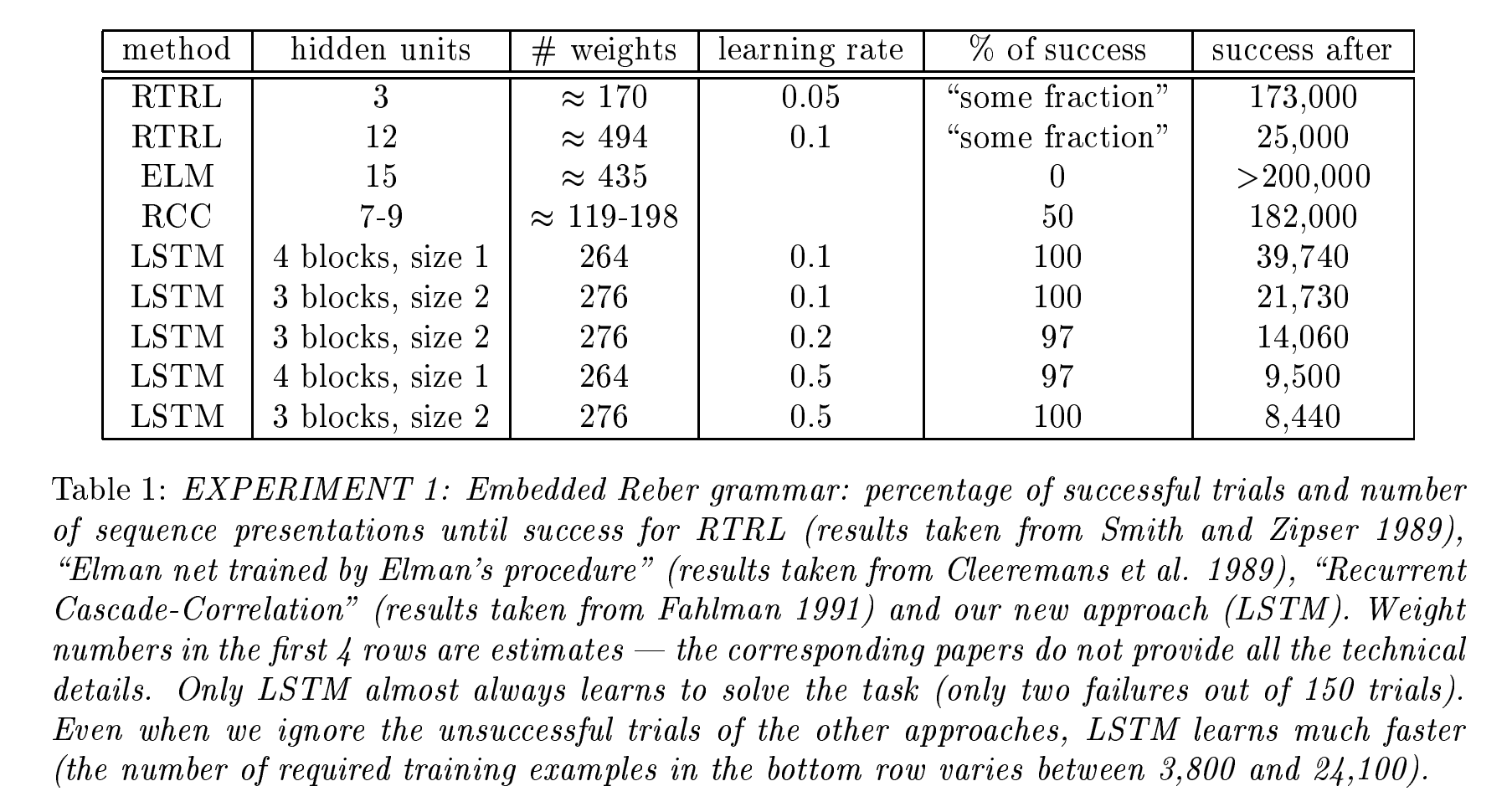
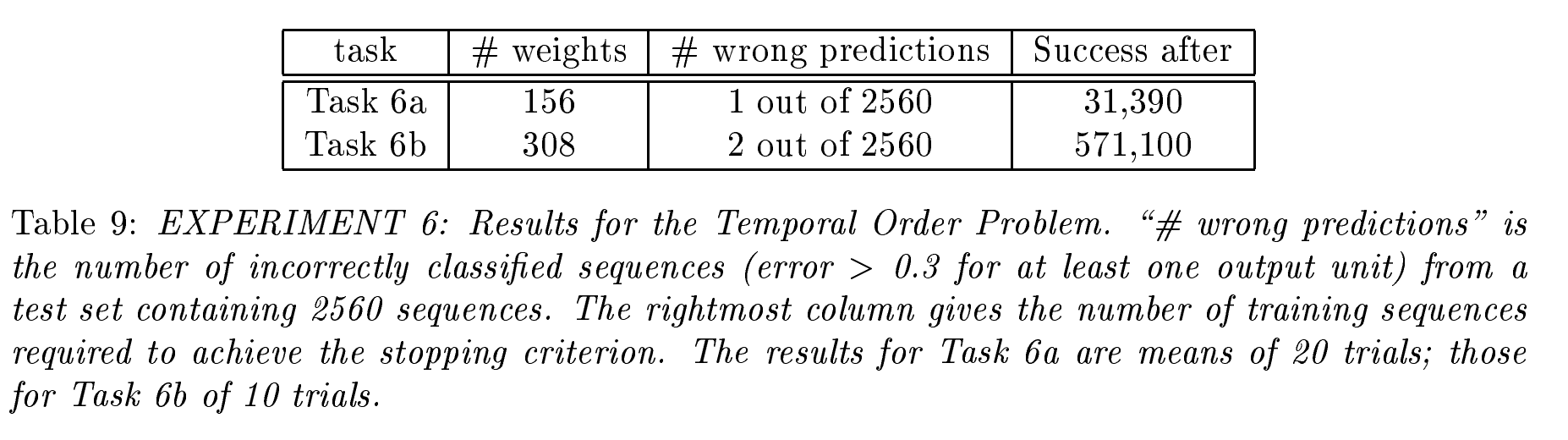
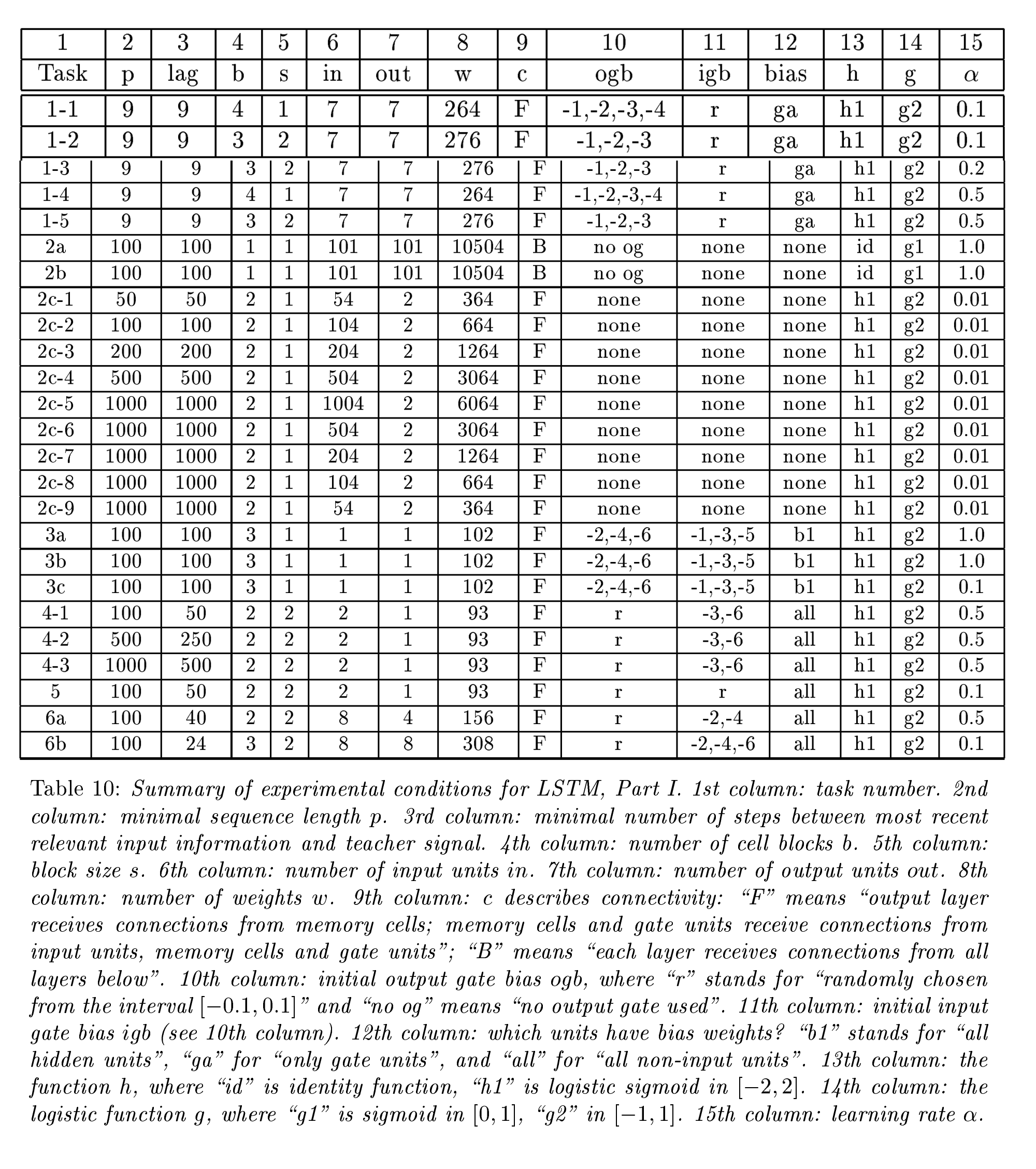
作者创建了6个具有不同时间延迟的序列数据集, 进行了6个不同级别的实验
| 实验 | 重点 | 关键细节 | 结果 | 其他评论 |
|---|---|---|---|---|
| 实验 1 | 基本的递归神经网络训练 | - 测试传统的递归神经网络(RNN)在简单时间序列问题中的表现 | - 递归神经网络(RNN)能够成功学习序列数据 | - 作为基线实验,用于对比LSTM和其他算法的表现 |
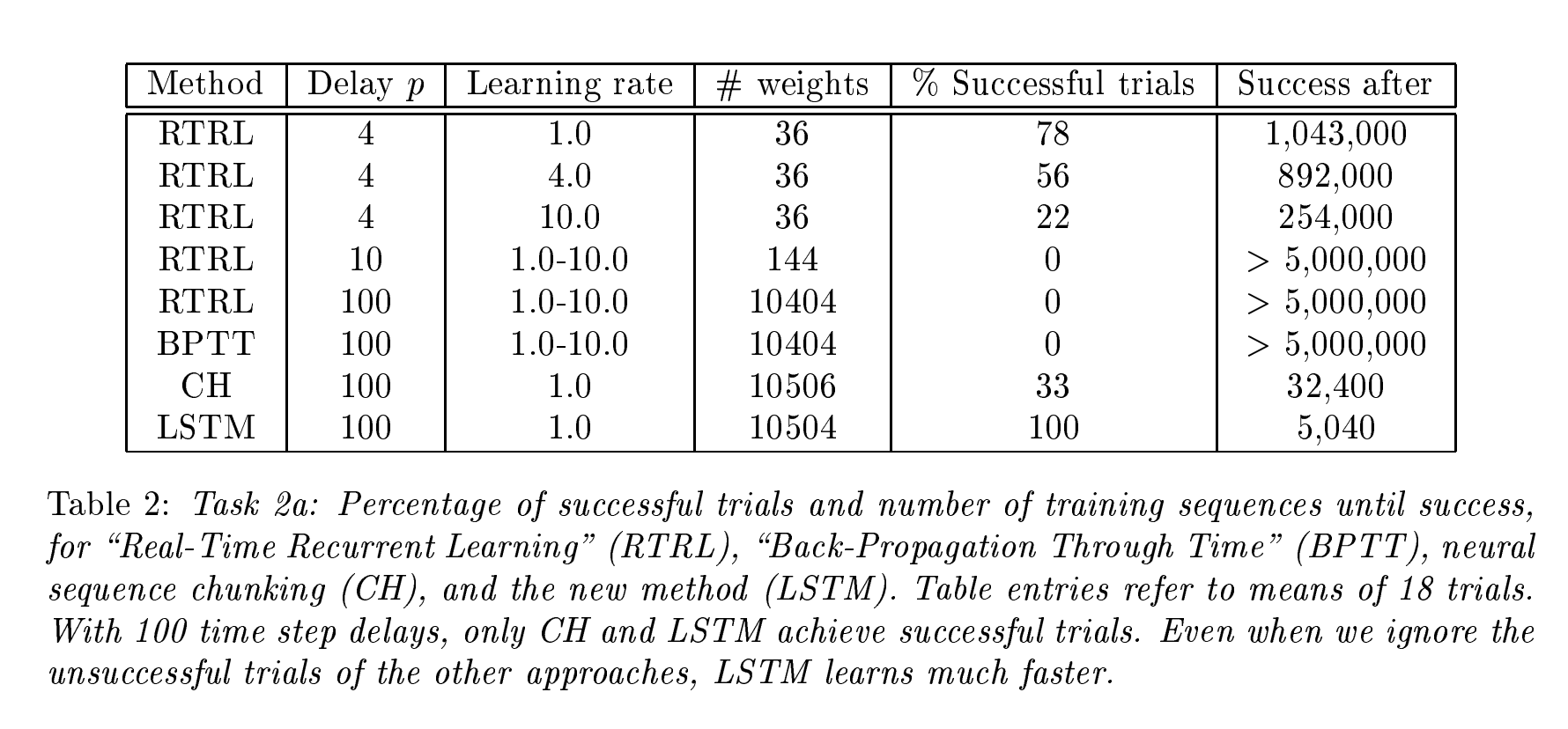
| 实验 2 | 无噪声和有噪声的序列,包含大量干扰符号 | - 任务 2c:成百上千个干扰符号,最小时间延迟为1000步 | - LSTM能够解决该问题 | - 在10步最小时间延迟下,BPTT和RIRL失败(参见Hochreiter 1991和Mozer 1992) |
| 实验 3 | 长时间延迟问题,信号和噪声同时存在 | - 3a/3b:Bengio等人的1994“2序列问题”(可以通过随机权重猜测快速解决) - 3c:更困难的2序列问题,需要学习带噪声目标的实值条件期望 |
- 随机权重猜测能解决简单的2序列问题 - 更复杂的2序列问题需要实值学习 |
|
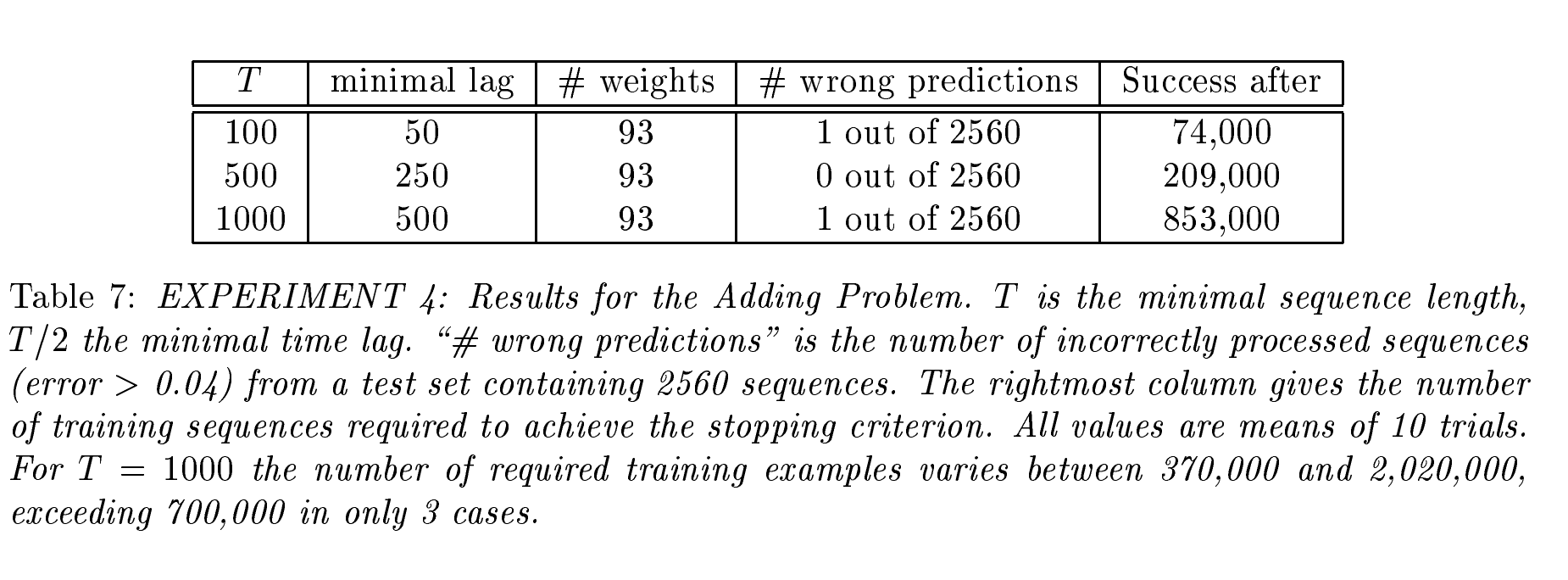
| 实验 4 和 5 | 分布式、连续值输入表示 | - 学习在长时间内存储精确的实值 - 相关输入信号可能出现在序列中的不同位置 |
- 最小时间延迟为几百步 | - 其他递归网络算法未能解决这些任务 |
| 实验 6 | 输入信号在序列中位置相距较远的复杂任务 | - 从输入的时间顺序中提取信息 | - LSTM成功解决任务 | - 其他递归网络算法未解决此类任务 |
- Embedded Reber Grammar:
- 普通的Reber Grammar:这是一个形式语法生成的序列,模型需要根据输入的符号序列预测下一个符号。这个任务主要是用于测试模型是否能捕捉到有限状态自动机(FSM)背后的结构。
- Reber Grammar的转移图如下所示:
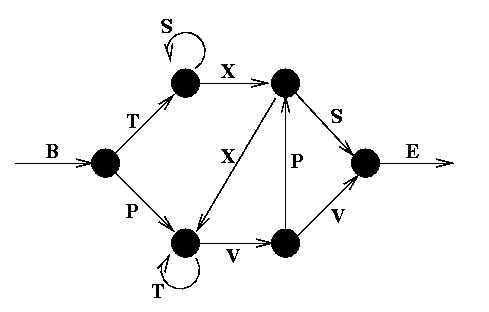
- Reber Grammar的转移图如下所示:
- 嵌入式Reber Grammar (Embedded Reber Grammar):在这个变体中,原本的Reber Grammar被嵌入到另一个任务中,要求模型不仅学习Reber Grammar的结构,还要学习如何从序列的不同位置提取出相关信息。这个任务比普通Reber Grammar更为复杂,因为它加入了更多的噪声和干扰符号。
- 嵌入式Reber Grammar的转移图如下所示:
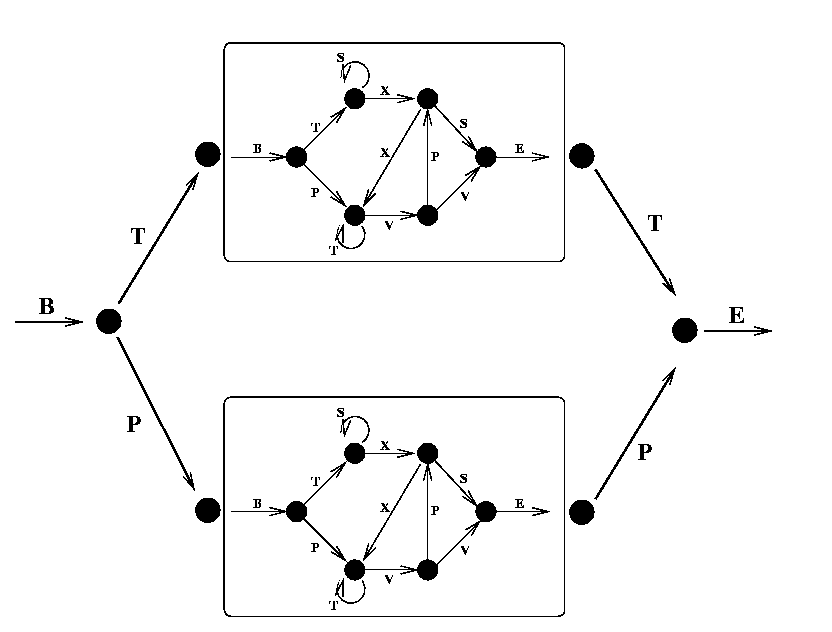
- 嵌入式Reber Grammar的转移图如下所示:
- 普通的Reber Grammar:这是一个形式语法生成的序列,模型需要根据输入的符号序列预测下一个符号。这个任务主要是用于测试模型是否能捕捉到有限状态自动机(FSM)背后的结构。
- 实验 2: 无噪声与有噪声的序列:
-
任务描述:实验 2 关注于无噪声和有噪声的序列数据,模型需要从包含大量干扰符号的序列中找到少数重要的符号。任务的难度在于,模型必须学会区分噪声和有意义的输入符号。
- 任务 2c:这是该实验中最困难的任务,要求模型从包含数百个干扰符号的长序列中学习。在这种情况下,干扰符号的位置是随机的,且最小时间间隔为1000步,这极大地增加了序列学习的复杂性。
- 规则:
-
- 生成训练序列的过程
- 序列前缀:首先随机生成一个长度为 \(q + 2\) 的序列前缀。
- 序列后缀:接着生成一个序列后缀,这个后缀包含一些额外的元素,这些元素不是 b、e、x 或 y,并且它们的生成概率是:
- 9/10 的概率生成任意符号(不等于 b、e、x、y)。
- 1/10 的概率生成符号 e。
当生成 e 时,序列会以 x 或 y 结束,这取决于序列中的第二个元素。
-
- 序列长度
- 最小序列长度:生成的序列的最小长度是 \(q + 4\)(即在序列前缀 \(q+2\) 基础上,加上至少两个符号)。
-
期望序列长度:在生成过程中,长度可能会随着随机生成的后缀而增加。我们需要计算这个期望长度。
-
- 期望长度的计算 期望序列长度是基于生成过程中的期望值来计算的。生成后缀的长度由随机变量控制,后缀长度为 \(k\),且 \(k\) 的概率分布是:\(k\) 以概率 \(\left(\frac{9}{10}\right)^k\) 生成,且后缀包含 \(k\) 个额外符号。
因此,期望长度的计算式是:
\[4 + \sum_{k=0}^{\infty} \frac{1}{10} \left( \frac{9}{10} \right)^k (q + k)\] -
-
- 实验 3: 噪声与信号位于同一输入线上的长时间延迟问题:
-
任务描述:实验 3 主要研究当噪声和信号同时出现在同一输入通道时,模型如何应对长时间的延迟。这是一个更具挑战性的任务,要求模型能够正确地从输入序列中提取出信号,并且忽略噪声。
-
任务 3a 和 3b:这些实验关注的是Bengio等人于1994年提出的“2-序列问题”,即模型需要从两个序列中提取出有意义的信息。这两个序列的特征可能是重复的,但它们有不同的时间延迟,模型必须能在给定时间间隔内捕捉到正确的关联。
-
任务 3c:该任务要求模型在具有较长时间延迟的情况下学习噪声目标的实值条件期望。这与传统的2-序列问题相比,更加困难,因为任务需要模型在给定输入序列的条件下估计出一个连续的目标值。
-
- 实验 4: 信号与噪声的同步问题:
- 任务描述:实验 4 探索了信号和噪声在时间轴上非常接近的情况,即信号与噪声几乎同步到达。模型需要分辨出信号并将其与背景噪声区分开来。该实验尤其关注模型在极短时间间隔内的反应能力。
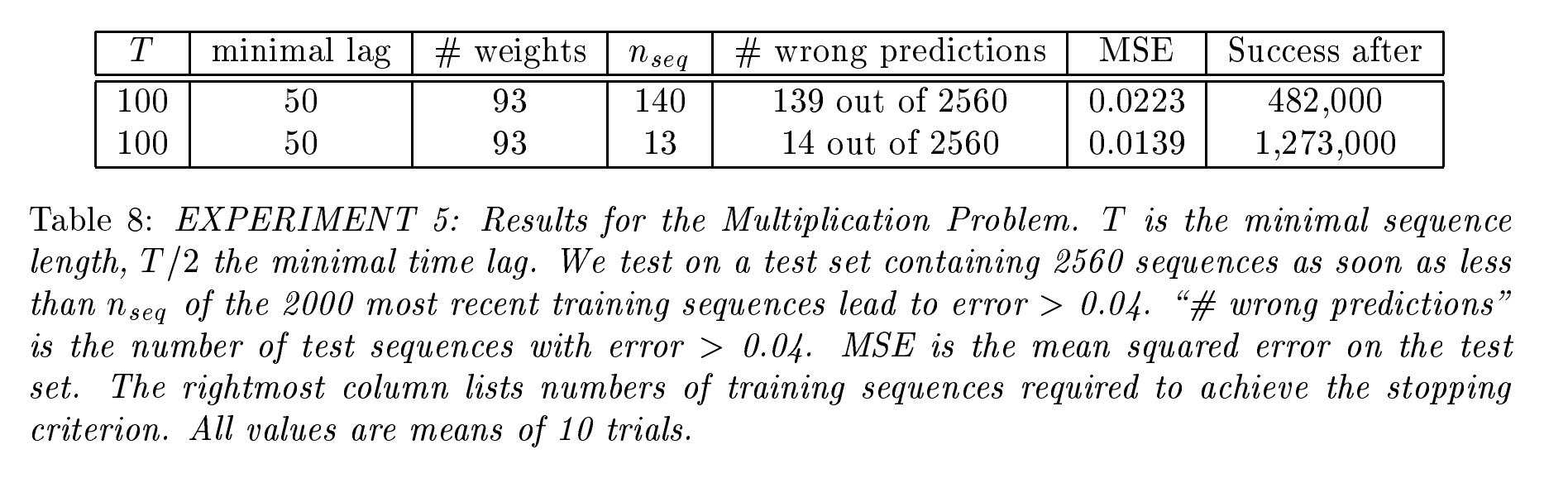
- 实验 5: 混合信号与复杂模式识别问题:
- 任务描述:在实验 5 中,信号与噪声的模式比以往更加复杂。模型不仅需要识别有意义的信号,还要处理复杂的干扰模式,这些干扰信号之间存在相互作用,增加了模式识别的难度。该实验的核心挑战是如何从多个交织的信号中提取出有用的信息。
- 实验 6: 输入信号在序列中位置相距较远的复杂任务:
- 任务描述:生成两条规则的序列
- 6a: E开头, B结尾, 长度100-110, 其余位置随机使用{a,b,c,d}集合中的任何一个字符, 其中随机在t1[10,20]和t2[50,60]位置,使用X或者Y.其中根据X, Y出现的前后顺序来决定它的分类,共4类{Q, R, S, U}. 分类规则是: X,X->Q; X,Y->R; Y,X->S; Y,Y->U;
- 6b: E开头, B结尾, 长度100-110, 其余位置随机使用{a,b,c,d}集合中的任何一个字符, 其中随机在t1[10,20], t2[33,43]和t3[66,76]位置,使用X或者Y.其中根据X, Y出现的前后顺序来决定它的分类,共8类{Q, R, S, U, V, A, B, C}. 分类规则是: X,X,X->Q; X,X,Y->R; X,Y,X->S; X,Y,Y->U; Y,X,X->V ; Y,X,Y->A; Y,Y,X->B; Y,Y,Y->C.
- 任务描述:生成两条规则的序列
效果
结构
- 原论文中,是没有遗忘门的,是后来引入的。
- 论文中使用的激活函数为特地构造的
- h function: \(h(x) = \frac{2}{1+e^{-x}}-1 \text{ , where h}\in [-1,1]\)
- g function: \(g(x) = \frac{4}{1+e^{-x}}-2 \text{ , where g}\in [-2,2]\)
- 使用截断反向传播(Truncated backprop)来防止梯度消失的问题: \(\begin{matrix} \frac{\partial net_{in_{j}}(t)}{y^u(t-1)}\approx \sideset{_{tr}}{}0, \forall u\\ \frac{\partial net_{out_{j}}(t)}{y^u(t-1)}\approx \sideset{_{tr}}{}0, \forall u \end{matrix}\)
- 接下来讨论的是以pytorch官方实现的LSTM结构做介绍
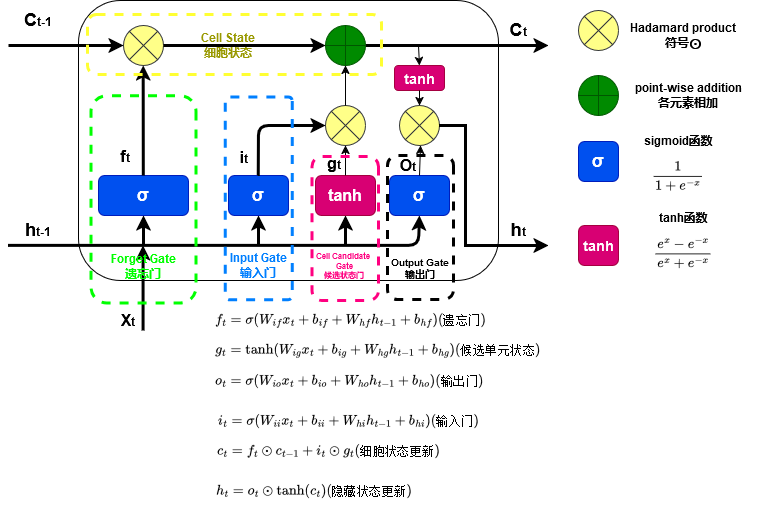
1. 组成部分
LSTM 的结构由记忆单元、门机制、状态更新构成:
1.1 记忆单元(Cell State)
- 是 LSTM 的核心部分,用于存储长期记忆信息。
- 信息通过加法操作沿时间步长传递,减轻了梯度消失问题。
1.2 门机制(Gates)
门机制控制信息的流动,决定了哪些信息需要保留,哪些需要丢弃。LSTM 包含以下三种门:
- 遗忘门(Forget Gate)
- 输入:当前时间步的输入 \(x_t\) 和前一时刻的隐藏状态 \(h_{t-1}\)。
- 输出:一个值范围在 (0,1) 的向量,表示每个单元的遗忘程度。
- 公式:\(f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf})\)
- 输入门(Input Gate)
- 确定哪些新信息需要写入记忆单元。
- 包含两部分:
- 更新信息的候选值。
- 选择需要更新的部分。
- 公式:\(i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi})\)
- 输出门(Output Gate)
- 确定当前时间步的隐藏状态输出 (h_t)。
- 公式:\(o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho})\)
1.3 状态更新
通过上述门机制更新记忆单元状态 和 隐藏状态:
- 记忆单元状态更新公式: \(c_t = f_t \odot c_{t-1} + i_t \odot g_t\)
- 隐藏状态更新公式: \(h_t = o_t \odot \tanh(c_t)\)
2. 数据流过程
- 输入当前时间步的数据 \(x_t\) 和上一时间步的隐藏状态 \(h_{t-1}\)。
- 通过遗忘门 \(f_t\) 决定哪些信息需要丢弃。
- 通过输入门 \(i_t\) 决定哪些新信息需要加入记忆单元。
- 更新记忆单元状态 \(c_t\)。
- 通过输出门 \(o_t\) 决定当前时间步的隐藏状态 \(h_t\)。
数学公式与推导
\[\begin{array}{ll} \\ i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) & (输入门)\\ f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) & (遗忘门)\\ g_t = \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) & (候选单元状态)\\ o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) & (输出门)\\ c_t = f_t \odot c_{t-1} + i_t \odot g_t & (单元状态更新)\\ h_t = o_t \odot \tanh(c_t) & (隐藏状态更新)\\ \end{array}\]- t: 第t时间。
- \(W\): 权重矩阵。
- \(W_{ii}\): 输入到输入门的权重。
- \(W_{hi}\): 前一个隐藏状态\(h_{t-1}\)到输入门的权重。
- \(W_{if}\): 输入到遗忘门的权重。
- \(W_{hf}\): 前一隐藏状态\(h_{t-1}\)到遗忘门的权重。
- \(W_{ig}\): 输入到候选单元状态的权重。
- \(W_{hg}\): 前一隐藏状态\(h_{t-1}\)到候选单元状态的权重。
- \(W_{io}\): 输入到输出门的权重。
- \(W_{ho}\): 前一隐藏状态\(h_{t-1}\)到输出门的权重。
- \(b\): 偏置。
- \(i_t\): 第t时刻的输入门的输出。
- \(f_t\): 第t时刻的遗忘门的输出。
- \(g_t\): 第t时刻的候选单元状态的输出。
- \(o_t\): 第t时刻的输出门的输出。
- \(h_t\): 第t时刻的隐藏状态。
- \(\sigma\): sigmoid 激活函数。
- \(\odot\): Hadamard product (element-wise product)。
- \(f_t \odot c_{t-1}\): t时刻遗忘门控制对于过去状态t-1的保留程度。
- \(i_t \odot g_t\): t时刻输入门控制对于当前候选状态的采纳程度。
LSTM反向传播梯度计算
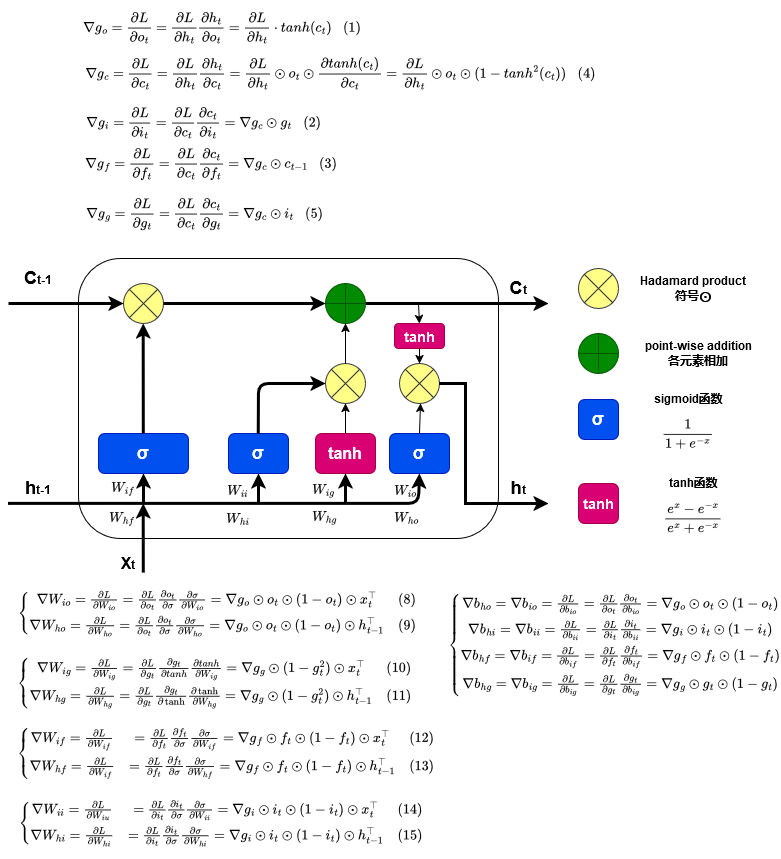
-
输出门的梯度 \(\begin{align} \nabla g_o =\frac{\partial L}{\partial o_t} &= \frac{\partial L}{\partial h_t}\frac{\partial h_t}{\partial o_t}=\frac{\partial L}{\partial h_t}\cdot tanh(c_t) \tag{1} \end{align}\)
-
输入门的梯度 \(\begin{align}\nabla g_i=\frac{\partial L}{\partial i_t}&=\frac{\partial L}{\partial c_t}\frac{\partial c_t}{\partial i_t}=\nabla g_c\odot g_t \tag{2}\end{align}\)
-
遗忘门的梯度 \(\begin{align}\nabla g_f=\frac{\partial L}{\partial f_t}&=\frac{\partial L}{\partial c_t}\frac{\partial c_t}{\partial f_t}=\nabla g_c\odot c_{t-1} \tag{3}\end{align}\)
-
记忆单元的梯度 \(\begin{align}\frac{\partial L}{\partial c_t}&=\frac{\partial L}{\partial h_t}\frac{\partial h_t}{\partial c_t}\\ &=\frac{\partial L}{\partial h_t}\odot o_t\odot \frac{\partial tanh(c_t)}{\partial c_t}\\ \nabla g_c&=\frac{\partial L}{\partial h_t}\odot o_t\odot(1-tanh^2(c_t))\tag{4}\end{align}\)
-
候选单元的梯度 \(\begin{align}\nabla g_g=\frac{\partial L}{\partial g_t}&=\frac{\partial L}{\partial c_t}\frac{\partial c_t}{\partial g_t}=\nabla g_c\odot i_t \tag{5}\end{align}\)
-
偏置的梯度 \(\left\{\begin{matrix} \nabla b_{ho}=\nabla b_{io} = \frac{\partial L}{\partial b_{io}}=\frac{\partial L}{\partial o_t}\frac{\partial o_t}{\partial b_{io}}=\nabla g_o \odot o_t\odot(1-o_t)\\ \nabla b_{hi}=\nabla b_{ii} = \frac{\partial L}{\partial b_{ii}}=\frac{\partial L}{\partial i_t}\frac{\partial i_t}{\partial b_{ii}}=\nabla g_i \odot i_t\odot(1-i_t)\\ \nabla b_{hf}=\nabla b_{if} = \frac{\partial L}{\partial b_{if}}=\frac{\partial L}{\partial f_t}\frac{\partial f_t}{\partial b_{if}}=\nabla g_f \odot f_t\odot(1-f_t)\\ \nabla b_{hg}=\nabla b_{ig} = \frac{\partial L}{\partial b_{ig}}=\frac{\partial L}{\partial g_t}\frac{\partial g_t}{\partial b_{ig}}=\nabla g_g \odot g_t\odot(1-g_t)\\ \end{matrix}\right.\)
-
更新\(W_{io}\)和\(W_{ho}\) \(\left\{\begin{matrix} \nabla W_{io}=\frac{\partial L}{\partial W_{io}}=\frac{\partial L}{\partial o_t}\frac{\partial o_t}{\partial \sigma}\frac{\partial \sigma}{\partial W_{io}} =\nabla g_o\odot o_t \odot (1-o_t )\odot x^\top_t & \text{(8)}\\ \nabla W_{ho}=\frac{\partial L}{\partial W_{ho}}=\frac{\partial L}{\partial o_t}\frac{\partial o_t}{\partial \sigma}\frac{\partial \sigma}{\partial W_{ho}} =\nabla g_o\odot o_t \odot (1-o_t )\odot h^\top_{t-1} & \text{(9)} \end{matrix}\right.\)
-
更新\(W_{ig}\)和\(W_{hg}\) \(\left\{\begin{matrix} \nabla W_{ig}=\frac{\partial L}{\partial W_{ig}}=\frac{\partial L}{\partial g_t}\frac{\partial g_t}{\partial tanh}\frac{\partial tanh}{\partial W_{ig}}=\nabla g_g \odot(1-g^2_t )\odot x^\top_t & \text{(10)}\\ \nabla W_{hg}=\frac{\partial L}{\partial W_{hg}}=\frac{\partial L}{\partial g_t}\frac{\partial g_t}{\partial \tanh}\frac{\partial \tanh}{\partial W_{hg}} =\nabla g_g \odot(1-g^2_t)\odot h^\top_{t-1} & \text{(11)} \end{matrix}\right.\)
-
更新\(W_{if}\)和\(W_{hf}\) \(\left\{\begin{matrix} \nabla W_{if}= \frac{\partial L}{\partial W_{if}}&=\frac{\partial L}{\partial f_{t}}\frac{\partial f_t}{\partial \sigma}\frac{\partial \sigma}{\partial W_{if}} =\nabla g_f\odot f_{t} \odot (1-f_{t} )\odot x^\top_t & \text{(12)}\\ \nabla W_{hf}= \frac{\partial L}{\partial W_{if}}&=\frac{\partial L}{\partial f_{t}}\frac{\partial f_t}{\partial \sigma}\frac{\partial \sigma}{\partial W_{hf}} =\nabla g_f\odot f_{t} \odot (1-f_{t} )\odot h^\top_{t-1} & \text{(13)} \end{matrix}\right.\)
-
更新\(W_{ii}\)和\(W_{hi}\) \(\left\{\begin{matrix} \nabla W_{ii}= \frac{\partial L}{\partial W_{iu}}&=\frac{\partial L}{\partial i_t}\frac{\partial i_t}{\partial \sigma}\frac{\partial \sigma}{\partial W_{ii}} =\nabla g_i \odot i_t \odot (1-i_t )\odot x^\top_t & \text{(14)}\\ \nabla W_{hi}= \frac{\partial L}{\partial W_{hi}}&=\frac{\partial L}{\partial i_t}\frac{\partial i_t}{\partial \sigma}\frac{\partial \sigma}{\partial W_{hi}} =\nabla g_i \odot i_t \odot (1-i_t )\odot h^\top_{t-1} & \text{(15)} \end{matrix}\right.\)
Code精读
- LSTM类 pytorch官方实现
- LSTM类 C++源码pytorch官方实现
- 第一个函数:适用于标准的固定长度序列输入,支持多种硬件平台的优化实现。
- 第二个函数:专为处理变长序列设计,使用 PackedSequence 来处理不同长度的序列数据,支持多种硬件平台的优化实现。
class LSTM(RNNBase):
r"""__init__(input_size,hidden_size,num_layers=1,bias=True,batch_first=False,dropout=0.0,bidirectional=False,proj_size=0,device=None,dtype=None)
Apply a multi-layer long short-term memory (LSTM) RNN to an input sequence.
For each element in the input sequence, each layer computes the following
function:
该方法将多层长短期记忆网络(LSTM)RNN 应用于输入序列。对于输入序列中的每个元素,每一层会计算以下公式:
.. math::
\begin{array}{ll} \\
i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\
f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\
g_t = \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) \\
o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) \\
c_t = f_t \odot c_{t-1} + i_t \odot g_t \\
h_t = o_t \odot \tanh(c_t) \\
\end{array}
where :math:`h_t` is the hidden state at time `t`, :math:`c_t` is the cell
state at time `t`, :math:`x_t` is the input at time `t`, :math:`h_{t-1}`
is the hidden state of the layer at time `t-1` or the initial hidden
state at time `0`, and :math:`i_t`, :math:`f_t`, :math:`g_t`,
:math:`o_t` are the input, forget, cell, and output gates, respectively.
:math:`\sigma` is the sigmoid function, and :math:`\odot` is the Hadamard product.
公式解释
- h_t :时间步 t 的隐藏状态。
- c_t :时间步 t 的记忆单元状态。
- x_t :时间步 t 的输入。
- h_{t-1} :时间步 t-1 的隐藏状态,或时间步 0 的初始隐藏状态。
- i_t 、 f_t 、 g_t 、 o_t :分别表示输入门、遗忘门、候选单元状态和输出门。
- \sigma :Sigmoid 函数。
- \odot :Hadamard 乘积(元素级乘积)。
In a multilayer LSTM, the input :math:`x^{(l)}_t` of the :math:`l` -th layer
(:math:`l \ge 2`) is the hidden state :math:`h^{(l-1)}_t` of the previous layer multiplied by
dropout :math:`\delta^{(l-1)}_t` where each :math:`\delta^{(l-1)}_t` is a Bernoulli random
variable which is :math:`0` with probability :attr:`dropout`.
在多层 LSTM 中,第 l 层的输入 x^{(l)}_t ( l \ge 2 )是前一层隐藏状态 h^{(l-1)}_t 与 dropout 掩码 \delta^{(l-1)}_t 的乘积,其中 \delta^{(l-1)}_t 是一个伯努利随机变量,概率为 `dropout` 时为 0 。
If ``proj_size > 0`` is specified, LSTM with projections will be used. This changes
the LSTM cell in the following way. First, the dimension of :math:`h_t` will be changed from
``hidden_size`` to ``proj_size`` (dimensions of :math:`W_{hi}` will be changed accordingly).
Second, the output hidden state of each layer will be multiplied by a learnable projection
matrix: :math:`h_t = W_{hr}h_t`. Note that as a consequence of this, the output
of LSTM network will be of different shape as well. See Inputs/Outputs sections below for exact
dimensions of all variables. You can find more details in https://arxiv.org/abs/1402.1128.
如果指定了 `proj_size > 0`,则会使用带有投影的 LSTM,其行为如下:
1. h_t 的维度将从 `hidden_size` 改为 `proj_size`( W_{hi} 的维度会相应调整)。
2. 每层的输出隐藏状态会乘以一个可学习的投影矩阵:
h_t = W_{hr} h_t
这会导致 LSTM 网络的输出形状发生变化。有关所有变量的确切维度,请参考输入/输出部分。更多细节请参阅https://arxiv.org/abs/1402.1128。
Args:
input_size: The number of expected features in the input `x`
hidden_size: The number of features in the hidden state `h`
num_layers: Number of recurrent layers. E.g., setting ``num_layers=2``
would mean stacking two LSTMs together to form a `stacked LSTM`,
with the second LSTM taking in outputs of the first LSTM and
computing the final results. Default: 1
bias: If ``False``, then the layer does not use bias weights `b_ih` and `b_hh`.
Default: ``True``
batch_first: If ``True``, then the input and output tensors are provided
as `(batch, seq, feature)` instead of `(seq, batch, feature)`.
Note that this does not apply to hidden or cell states. See the
Inputs/Outputs sections below for details. Default: ``False``
dropout: If non-zero, introduces a `Dropout` layer on the outputs of each
LSTM layer except the last layer, with dropout probability equal to
:attr:`dropout`. Default: 0
bidirectional: If ``True``, becomes a bidirectional LSTM. Default: ``False``
proj_size: If ``> 0``, will use LSTM with projections of corresponding size. Default: 0
- **`input_size`**: 输入 x 中预期的特征数。
- **`hidden_size`**: 隐藏状态 h 中的特征数。
- **`num_layers`**: 循环层的数量。例如,设置 `num_layers=2` 意味着将两个 LSTM 堆叠在一起形成一个“堆叠 LSTM”(stacked LSTM),第二个 LSTM 以第一个 LSTM 的输出作为输入并计算最终结果。默认值:1。
- **`bias`**: 如果设置为 `False`,则该层不会使用偏置权重 b_{ih} 和 b_{hh}。默认值:`True`。
- **`batch_first`**: 如果设置为 `True`,则输入和输出张量的维度格式为 `(batch, seq, feature)`,而不是 `(seq, batch, feature)`。注意,这不适用于隐藏状态或记忆单元状态。详情请参考输入/输出部分。默认值:`False`。
- **`dropout`**: 如果非零,在每层 LSTM 的输出(除最后一层外)上添加一个 Dropout 层,其丢弃概率等于 `dropout` 参数值。默认值:0。
- **`bidirectional`**: 如果设置为 `True`,则使用双向 LSTM。默认值:`False`。
- **`proj_size`**: 如果设置为大于 0 的值,则使用具有对应大小投影的 LSTM。默认值:0。
Inputs: input, (h_0, c_0)
* **input**: tensor of shape :math:`(L, H_{in})` for unbatched input,
:math:`(L, N, H_{in})` when ``batch_first=False`` or
:math:`(N, L, H_{in})` when ``batch_first=True`` containing the features of
the input sequence. The input can also be a packed variable length sequence.
See :func:`torch.nn.utils.rnn.pack_padded_sequence` or
:func:`torch.nn.utils.rnn.pack_sequence` for details.
* **h_0**: tensor of shape :math:`(D * \text{num\_layers}, H_{out})` for unbatched input or
:math:`(D * \text{num\_layers}, N, H_{out})` containing the
initial hidden state for each element in the input sequence.
Defaults to zeros if (h_0, c_0) is not provided.
* **c_0**: tensor of shape :math:`(D * \text{num\_layers}, H_{cell})` for unbatched input or
:math:`(D * \text{num\_layers}, N, H_{cell})` containing the
initial cell state for each element in the input sequence.
Defaults to zeros if (h_0, c_0) is not provided.
- **`input`**:
一个张量,表示输入序列的特征,形状如下:
- 未分批输入时,形状为 \( (L, H_{in}) \);
- 当 `batch_first=False` 时,形状为 \( (L, N, H_{in}) \);
- 当 `batch_first=True` 时,形状为 \( (N, L, H_{in}) \)。
输入也可以是一个打包的变长序列。详情请参见函数 [`torch.nn.utils.rnn.pack_padded_sequence`](https://pytorch.org/docs/stable/generated/torch.nn.utils.rnn.pack_padded_sequence.html) 或 [`torch.nn.utils.rnn.pack_sequence`](https://pytorch.org/docs/stable/generated/torch.nn.utils.rnn.pack_sequence.html)。
- **`h_0`**:
一个张量,表示输入序列中每个元素的初始隐藏状态,形状如下:
- 未分批输入时,形状为 \( (D \times \text{num\_layers}, H_{out}) \);
- 分批输入时,形状为 \( (D \times \text{num\_layers}, N, H_{out}) \)。
如果未提供 `(h_0, c_0)`,默认值为全零。
- **`c_0`**:
一个张量,表示输入序列中每个元素的初始记忆单元状态,形状如下:
- 未分批输入时,形状为 \( (D \times \text{num\_layers}, H_{cell}) \);
- 分批输入时,形状为 \( (D \times \text{num\_layers}, N, H_{cell}) \)。
如果未提供 `(h_0, c_0)`,默认值为全零。
where:
.. math::
\begin{aligned}
N ={} & \text{batch size} \\
L ={} & \text{sequence length} \\
D ={} & 2 \text{ if bidirectional=True otherwise } 1 \\
H_{in} ={} & \text{input\_size} \\
H_{cell} ={} & \text{hidden\_size} \\
H_{out} ={} & \text{proj\_size if } \text{proj\_size}>0 \text{ otherwise hidden\_size} \\
\end{aligned}
Outputs: output, (h_n, c_n)
* **output**: tensor of shape :math:`(L, D * H_{out})` for unbatched input,
:math:`(L, N, D * H_{out})` when ``batch_first=False`` or
:math:`(N, L, D * H_{out})` when ``batch_first=True`` containing the output features
`(h_t)` from the last layer of the LSTM, for each `t`. If a
:class:`torch.nn.utils.rnn.PackedSequence` has been given as the input, the output
will also be a packed sequence. When ``bidirectional=True``, `output` will contain
a concatenation of the forward and reverse hidden states at each time step in the sequence.
* **h_n**: tensor of shape :math:`(D * \text{num\_layers}, H_{out})` for unbatched input or
:math:`(D * \text{num\_layers}, N, H_{out})` containing the
final hidden state for each element in the sequence. When ``bidirectional=True``,
`h_n` will contain a concatenation of the final forward and reverse hidden states, respectively.
* **c_n**: tensor of shape :math:`(D * \text{num\_layers}, H_{cell})` for unbatched input or
:math:`(D * \text{num\_layers}, N, H_{cell})` containing the
final cell state for each element in the sequence. When ``bidirectional=True``,
`c_n` will contain a concatenation of the final forward and reverse cell states, respectively.
- **`output`**:
一个张量,表示 LSTM 最后一层对每个时间步 `t` 计算得到的输出特征 `(h_t)`,其形状如下:
- 未分批输入时,形状为 \( (L, D \times H_{out}) \);
- 当 `batch_first=False` 时,形状为 \( (L, N, D \times H_{out}) \);
- 当 `batch_first=True` 时,形状为 \( (N, L, D \times H_{out}) \)。
如果输入是一个 :class:`torch.nn.utils.rnn.PackedSequence`,输出也将是一个打包序列。当 `bidirectional=True` 时,`output` 将包含在序列中每个时间步的前向和反向隐藏状态的拼接。
- **`h_n`**:
一个张量,表示序列中每个元素的最终隐藏状态,形状如下:
- 未分批输入时,形状为 \( (D \times \text{num\_layers}, H_{out}) \);
- 分批输入时,形状为 \( (D \times \text{num\_layers}, N, H_{out}) \)。
当 `bidirectional=True` 时,`h_n` 将包含最终前向和反向隐藏状态的拼接。
- **`c_n`**:
一个张量,表示序列中每个元素的最终记忆单元状态,形状如下:
- 未分批输入时,形状为 \( (D \times \text{num\_layers}, H_{cell}) \);
- 分批输入时,形状为 \( (D \times \text{num\_layers}, N, H_{cell}) \)。
当 `bidirectional=True` 时,`c_n` 将包含最终前向和反向记忆单元状态的拼接。
Attributes:
weight_ih_l[k] : the learnable input-hidden weights of the :math:`\text{k}^{th}` layer
`(W_ii|W_if|W_ig|W_io)`, of shape `(4*hidden_size, input_size)` for `k = 0`.
Otherwise, the shape is `(4*hidden_size, num_directions * hidden_size)`. If
``proj_size > 0`` was specified, the shape will be
`(4*hidden_size, num_directions * proj_size)` for `k > 0`
weight_hh_l[k] : the learnable hidden-hidden weights of the :math:`\text{k}^{th}` layer
`(W_hi|W_hf|W_hg|W_ho)`, of shape `(4*hidden_size, hidden_size)`. If ``proj_size > 0``
was specified, the shape will be `(4*hidden_size, proj_size)`.
bias_ih_l[k] : the learnable input-hidden bias of the :math:`\text{k}^{th}` layer
`(b_ii|b_if|b_ig|b_io)`, of shape `(4*hidden_size)`
bias_hh_l[k] : the learnable hidden-hidden bias of the :math:`\text{k}^{th}` layer
`(b_hi|b_hf|b_hg|b_ho)`, of shape `(4*hidden_size)`
weight_hr_l[k] : the learnable projection weights of the :math:`\text{k}^{th}` layer
of shape `(proj_size, hidden_size)`. Only present when ``proj_size > 0`` was
specified.
weight_ih_l[k]_reverse: Analogous to `weight_ih_l[k]` for the reverse direction.
Only present when ``bidirectional=True``.
weight_hh_l[k]_reverse: Analogous to `weight_hh_l[k]` for the reverse direction.
Only present when ``bidirectional=True``.
bias_ih_l[k]_reverse: Analogous to `bias_ih_l[k]` for the reverse direction.
Only present when ``bidirectional=True``.
bias_hh_l[k]_reverse: Analogous to `bias_hh_l[k]` for the reverse direction.
Only present when ``bidirectional=True``.
weight_hr_l[k]_reverse: Analogous to `weight_hr_l[k]` for the reverse direction.
Only present when ``bidirectional=True`` and ``proj_size > 0`` was specified.
.. note::
All the weights and biases are initialized from :math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})`
where :math:`k = \frac{1}{\text{hidden\_size}}`
权重和偏置的初始化均采用
.. note::
For bidirectional LSTMs, forward and backward are directions 0 and 1 respectively.
Example of splitting the output layers when ``batch_first=False``:
``output.view(seq_len, batch, num_directions, hidden_size)``.
双向 RNN 的前向和后向方向分别用方向编号 0 和 1 表示。
.. note::
For bidirectional LSTMs, `h_n` is not equivalent to the last element of `output`; the
former contains the final forward and reverse hidden states, while the latter contains the
final forward hidden state and the initial reverse hidden state.
.. note::
``batch_first`` argument is ignored for unbatched inputs.
.. note::
``proj_size`` should be smaller than ``hidden_size``.
.. include:: ../cudnn_rnn_determinism.rst
.. include:: ../cudnn_persistent_rnn.rst
Examples::
>>> rnn = nn.LSTM(10, 20, 2)
>>> input = torch.randn(5, 3, 10)
>>> h0 = torch.randn(2, 3, 20)
>>> c0 = torch.randn(2, 3, 20)
>>> output, (hn, cn) = rnn(input, (h0, c0))
"""
@overload
def __init__(
self,
input_size: int,
hidden_size: int,
num_layers: int = 1,
bias: bool = True,
batch_first: bool = False,
dropout: float = 0.0,
bidirectional: bool = False,
proj_size: int = 0,
device=None,
dtype=None,
) -> None:
...
@overload
def __init__(self, *args, **kwargs):
...
def __init__(self, *args, **kwargs):
super().__init__("LSTM", *args, **kwargs)
def get_expected_cell_size(
self, input: Tensor, batch_sizes: Optional[Tensor]
) -> tuple[int, int, int]:
if batch_sizes is not None:
mini_batch = int(batch_sizes[0])
else:
mini_batch = input.size(0) if self.batch_first else input.size(1)
num_directions = 2 if self.bidirectional else 1
expected_hidden_size = (
self.num_layers * num_directions,
mini_batch,
self.hidden_size,
)
return expected_hidden_size
# In the future, we should prevent mypy from applying contravariance rules here.
# See torch/nn/modules/module.py::_forward_unimplemented
def check_forward_args(
self,
input: Tensor,
hidden: tuple[Tensor, Tensor], # type: ignore[override]
batch_sizes: Optional[Tensor],
):
self.check_input(input, batch_sizes)
self.check_hidden_size(
hidden[0],
self.get_expected_hidden_size(input, batch_sizes),
"Expected hidden[0] size {}, got {}",
)
self.check_hidden_size(
hidden[1],
self.get_expected_cell_size(input, batch_sizes),
"Expected hidden[1] size {}, got {}",
)
# Same as above, see torch/nn/modules/module.py::_forward_unimplemented
def permute_hidden( # type: ignore[override]
self,
hx: tuple[Tensor, Tensor],
permutation: Optional[Tensor],
) -> tuple[Tensor, Tensor]:
if permutation is None:
return hx
return _apply_permutation(hx[0], permutation), _apply_permutation(
hx[1], permutation
)
# Same as above, see torch/nn/modules/module.py::_forward_unimplemented
@overload # type: ignore[override]
@torch._jit_internal._overload_method # noqa: F811
def forward(
self, input: Tensor, hx: Optional[tuple[Tensor, Tensor]] = None
) -> tuple[Tensor, tuple[Tensor, Tensor]]: # noqa: F811
pass
# Same as above, see torch/nn/modules/module.py::_forward_unimplemented
@overload
@torch._jit_internal._overload_method # noqa: F811
def forward(
self, input: PackedSequence, hx: Optional[tuple[Tensor, Tensor]] = None
) -> tuple[PackedSequence, tuple[Tensor, Tensor]]: # noqa: F811
pass
def forward(self, input, hx=None): # noqa: F811
self._update_flat_weights()
orig_input = input
# xxx: isinstance check needs to be in conditional for TorchScript to compile
batch_sizes = None
num_directions = 2 if self.bidirectional else 1
real_hidden_size = self.proj_size if self.proj_size > 0 else self.hidden_size
if isinstance(orig_input, PackedSequence):
input, batch_sizes, sorted_indices, unsorted_indices = input
max_batch_size = batch_sizes[0]
if hx is None:
h_zeros = torch.zeros(
self.num_layers * num_directions,
max_batch_size,
real_hidden_size,
dtype=input.dtype,
device=input.device,
)
c_zeros = torch.zeros(
self.num_layers * num_directions,
max_batch_size,
self.hidden_size,
dtype=input.dtype,
device=input.device,
)
hx = (h_zeros, c_zeros)
else:
# Each batch of the hidden state should match the input sequence that
# the user believes he/she is passing in.
hx = self.permute_hidden(hx, sorted_indices)
else:
if input.dim() not in (2, 3):
raise ValueError(
f"LSTM: Expected input to be 2D or 3D, got {input.dim()}D instead"
)
is_batched = input.dim() == 3
batch_dim = 0 if self.batch_first else 1
if not is_batched:
input = input.unsqueeze(batch_dim)
max_batch_size = input.size(0) if self.batch_first else input.size(1)
sorted_indices = None
unsorted_indices = None
if hx is None:
h_zeros = torch.zeros(
self.num_layers * num_directions,
max_batch_size,
real_hidden_size,
dtype=input.dtype,
device=input.device,
)
c_zeros = torch.zeros(
self.num_layers * num_directions,
max_batch_size,
self.hidden_size,
dtype=input.dtype,
device=input.device,
)
hx = (h_zeros, c_zeros)
self.check_forward_args(input, hx, batch_sizes)
else:
if is_batched:
if hx[0].dim() != 3 or hx[1].dim() != 3:
msg = (
"For batched 3-D input, hx and cx should "
f"also be 3-D but got ({hx[0].dim()}-D, {hx[1].dim()}-D) tensors"
)
raise RuntimeError(msg)
else:
if hx[0].dim() != 2 or hx[1].dim() != 2:
msg = (
"For unbatched 2-D input, hx and cx should "
f"also be 2-D but got ({hx[0].dim()}-D, {hx[1].dim()}-D) tensors"
)
raise RuntimeError(msg)
hx = (hx[0].unsqueeze(1), hx[1].unsqueeze(1))
# Each batch of the hidden state should match the input sequence that
# the user believes he/she is passing in.
self.check_forward_args(input, hx, batch_sizes)
hx = self.permute_hidden(hx, sorted_indices)
if batch_sizes is None:
result = _VF.lstm(
input,
hx,
self._flat_weights, # type: ignore[arg-type]
self.bias,
self.num_layers,
self.dropout,
self.training,
self.bidirectional,
self.batch_first,
)
else:
result = _VF.lstm(
input,
batch_sizes,
hx,
self._flat_weights, # type: ignore[arg-type]
self.bias,
self.num_layers,
self.dropout,
self.training,
self.bidirectional,
)
output = result[0]
hidden = result[1:]
# xxx: isinstance check needs to be in conditional for TorchScript to compile
if isinstance(orig_input, PackedSequence):
output_packed = PackedSequence(
output, batch_sizes, sorted_indices, unsorted_indices
)
return output_packed, self.permute_hidden(hidden, unsorted_indices)
else:
if not is_batched: # type: ignore[possibly-undefined]
output = output.squeeze(batch_dim) # type: ignore[possibly-undefined]
hidden = (hidden[0].squeeze(1), hidden[1].squeeze(1))
return output, self.permute_hidden(hidden, unsorted_indices)
// 定义 LSTMCell 结构体,继承自 Cell 类,返回类型为 std::tuple<Tensor, Tensor>
struct LSTMCell : Cell<std::tuple<Tensor, Tensor>, cell_params> {
// 定义 hidden_type 为 std::tuple<Tensor, Tensor>,用于存储隐藏状态 (hx) 和细胞状态 (cx)
using hidden_type = std::tuple<Tensor, Tensor>;
// 重载 operator(),实现 LSTM 单元的前向计算
hidden_type operator()(
const Tensor& input, // 输入张量
const hidden_type& hidden, // 隐藏状态 (hx, cx)
const cell_params& params, // LSTM 参数,包括权重和偏置
bool pre_compute_input = false) const override {
// 解包 hidden 为 hx (隐藏状态) 和 cx (细胞状态)
const auto& [hx, cx] = hidden;
// 如果输入张量是在 CUDA 或 XPU 或特殊私有设备上,则执行 GPU 加速路径
if (input.is_cuda() || input.is_xpu() || input.is_privateuseone()) {
// 检查 pre_compute_input 是否为 false
TORCH_CHECK(!pre_compute_input);
// 计算输入门和隐藏状态门的线性变换
auto igates = params.matmul_ih(input); // 输入与权重矩阵的乘法
auto hgates = params.matmul_hh(hx); // 隐藏状态与权重矩阵的乘法
// 调用 fused LSTM cell 函数,执行 LSTM 的前向计算
auto result = at::_thnn_fused_lstm_cell(
igates, hgates, cx, params.b_ih(), params.b_hh()); // 参数包括输入门、隐藏状态门、细胞状态等
// 如果定义了 w_hr,应用投影
auto hy = params.matmul_hr(std::get<0>(result)); // 计算隐藏层输出
// 返回包含更新后的隐藏状态 (hy) 和细胞状态 (cy)
return std::make_tuple(std::move(hy), std::move(std::get<1>(result)));
}
// 对于 CPU 路径,先计算输入门和隐藏门的线性变换
const auto gates = params.linear_hh(hx).add_(
pre_compute_input ? input : params.linear_ih(input)); // 线性变换,并加上输入门的偏置
// 将计算的门值从列维度分割成 4 个部分:输入门、遗忘门、细胞门和输出门
auto chunked_gates = gates.unsafe_chunk(4, 1);
// 对每个门应用激活函数:输入门和遗忘门使用 sigmoid,细胞门使用 tanh,输出门使用 sigmoid
auto ingate = chunked_gates[0].sigmoid_();
auto forgetgate = chunked_gates[1].sigmoid_();
auto cellgate = chunked_gates[2].tanh_();
auto outgate = chunked_gates[3].sigmoid_();
// 计算细胞状态:cy = f_t * c_{t-1} + i_t * tanh(c_t)
auto cy = (forgetgate * cx).add_(ingate * cellgate);
// 计算隐藏状态:hy = o_t * tanh(c_t)
auto hy = outgate * cy.tanh();
// 通过权重矩阵 w_hr 进行投影,生成最终的隐藏状态
hy = params.matmul_hr(hy);
// 返回更新后的隐藏状态和细胞状态
return std::make_tuple(std::move(hy), std::move(cy));
}
};
std::tuple<Tensor, Tensor> lstm_cell(
const Tensor& input, TensorList hx,//hx:一个包含 LSTM 隐藏状态和细胞状态的张量列表。
const Tensor& w_ih, const Tensor& w_hh, const std::optional<Tensor>& b_ih_opt, const std::optional<Tensor>& b_hh_opt) {
// See [Note: hacky wrapper removal for optional tensor]
c10::MaybeOwned<Tensor> b_ih_maybe_owned = at::borrow_from_optional_tensor(b_ih_opt);
const Tensor& b_ih = *b_ih_maybe_owned;
const Tensor& b_hh = b_hh_opt.value_or(Tensor());
TORCH_CHECK(hx.size() == 2, "lstm_cell expects two hidden states");
check_rnn_cell_forward_input(input, w_ih.sym_size(1));//检查输入的尺寸是否与 w_ih 的期望尺寸匹配。
auto hidden_size = w_hh.sym_size(1);
//检查 LSTM 的前一个隐藏状态和细胞状态的尺寸是否符合要求。
check_rnn_cell_forward_hidden(input, hx[0], hidden_size, 0);//hx[0]是上一个时间步的隐藏状态h_{t-1}。
check_rnn_cell_forward_hidden(input, hx[1], std::move(hidden_size), 1);//hx[1]是上一个时间步的细胞状态 c_{t-1}。
static at::Tensor undefined;
return LSTMCell<CellParams>{}(input, std::make_tuple(hx[0], hx[1]), CellParams{w_ih, w_hh, b_ih, b_hh, undefined});
}
_thnn_differentiable_lstm_cell_backward( const std::optional<Tensor>& grad_hy_opt, const std::optional<Tensor>& grad_cy_opt,
const Tensor& input_gates,
const Tensor& hidden_gates, const std::optional<Tensor>& input_bias_opt, const std::optional<Tensor>& hidden_bias_opt,
const Tensor& cx,
const Tensor& cy) {
/* See [Note: hacky wrapper removal for optional tensor]
grad_hy_opt:可选的 LSTM 输出隐藏状态的梯度 grad_hy,对应于 h_t。
grad_cy_opt:可选的 LSTM 输出细胞状态的梯度 grad_cy,对应于 c_t。
input_gates:输入门的计算结果,即 W_ii * x_t + b_ii + W_hi * h_{t-1} + b_hi,这在前向传播时计算并传入。
hidden_gates:隐藏门的计算结果,即 W_hi * h_{t-1} + b_hi。
input_bias_opt:可选的输入偏置项。
hidden_bias_opt:可选的隐藏偏置项。
cx:前一时刻的细胞状态 c_{t-1}。
cy:当前时刻的细胞状态 c_t。 */
c10::MaybeOwned<Tensor> grad_hy_maybe_owned = at::borrow_from_optional_tensor(grad_hy_opt);
const Tensor& grad_hy = *grad_hy_maybe_owned;
const Tensor& grad_cy = grad_cy_opt.value_or(Tensor());
const Tensor& input_bias = input_bias_opt.value_or(Tensor());
const Tensor& hidden_bias = hidden_bias_opt.value_or(Tensor());
//如果 grad_hy 和 grad_cy 都没有定义,则直接返回一个包含五个张量的空元组
if (!grad_hy.defined() && !grad_cy.defined()) {
return std::tuple<Tensor, Tensor, Tensor, Tensor, Tensor>();
}
//将输入门(input_gates)和隐藏门(hidden_gates)相加,得到总的门值(gates)
Tensor gates = input_gates + hidden_gates;
//如果定义了偏置项,则将其加到 gates 中
if (input_bias.defined()) {
gates = gates + input_bias;
}
if (hidden_bias.defined()) {
gates = gates + hidden_bias;
}
//然后将 gates 分成四个部分:i(输入门),f(遗忘门),c(细胞候选值),o(输出门)。
auto chunked_gates = gates.unsafe_chunk(4, 1);
Tensor i = chunked_gates[0].sigmoid();
Tensor f = chunked_gates[1].sigmoid();
Tensor c = chunked_gates[2].tanh();
Tensor o = chunked_gates[3].sigmoid();
//gcx:细胞状态的梯度初始化为当前时刻细胞状态 cy 的 tanh 结果
Tensor gcx = cy.tanh();
Tensor gog;
TORCH_INTERNAL_ASSERT((grad_hy.defined() || grad_cy.defined()),"either gradient with respect to hy or cy should be defined");
if (grad_hy.defined()) {
//计算 gog,它是 grad_hy 和 gcx 的乘积,然后计算输出门 o 的反向传播梯度
gog = grad_hy * gcx;
gog = at::sigmoid_backward(gog, o);
//将细胞状态 gcx 的梯度更新为当前时刻的 grad_hy 和输出门 o 的乘积,并进行反向传播。
gcx = at::tanh_backward(grad_hy * o, gcx);
//如果 grad_cy 已定义,则将其加到 gcx 中
if (grad_cy.defined()) {
gcx = gcx + grad_cy;
}
//如果只有 grad_cy 被定义,则 gog 初始化为零,gcx 直接等于 grad_cy。
} else if (grad_cy.defined()) {
gog = at::zeros_like(cx, LEGACY_CONTIGUOUS_MEMORY_FORMAT);
gcx = grad_cy;
}
//gig:输入门的梯度
Tensor gig = gcx * c;
//gfg:遗忘门的梯度
Tensor gfg = gcx * cx;
//gcg:细胞候选值的梯度
Tensor gcg = gcx * i;
gcx = gcx * f;
//对每个门的梯度进行反向传播计算
gig = at::sigmoid_backward(gig, i);
gfg = at::sigmoid_backward(gfg, f);
gcg = at::tanh_backward(gcg, c);
//将计算出的梯度拼接成一个张量 grad_gates,其中包含了所有门(i、f、c、o)的梯度。std::move 被用来将 Tensor 或其他对象的所有权从一个函数传递到另一个函数中,避免不必要的内存复制
Tensor grad_gates = at::cat({std::move(gig), std::move(gfg), std::move(gcg), std::move(gog)}, 1);
//如果输入偏置存在,计算其梯度,即所有门的梯度沿着第一个维度求和,得到 grad_bias。
Tensor grad_bias = input_bias.defined() ? grad_gates.sum(0, /*keepdim=*/false) : at::Tensor{};
return std::make_tuple(grad_gates, grad_gates, std::move(gcx), grad_bias, grad_bias);
}
class RNN(RNNBase):
r"""__init__(input_size,hidden_size,num_layers=1,nonlinearity='tanh',bias=True,batch_first=False,dropout=0.0,bidirectional=False,device=None,dtype=None)
Apply a multi-layer Elman RNN with :math:`\tanh` or :math:`\text{ReLU}`
non-linearity to an input sequence. For each element in the input sequence,
each layer computes the following function:
对输入序列应用多层 Elman RNN,使用 \(\tanh\) 或 \(\text{ReLU}\) 作为非线性激活函数。对于输入序列中的每一个元素,每一层计算如下公式:
.. math::
h_t = \tanh(x_t W_{ih}^T + b_{ih} + h_{t-1}W_{hh}^T + b_{hh})
where :math:`h_t` is the hidden state at time `t`, :math:`x_t` is
the input at time `t`, and :math:`h_{(t-1)}` is the hidden state of the
previous layer at time `t-1` or the initial hidden state at time `0`.
If :attr:`nonlinearity` is ``'relu'``, then :math:`\text{ReLU}` is used instead of :math:`\tanh`.
.. code-block:: python
# Efficient implementation equivalent to the following with bidirectional=False
# 以下代码块展示了无双向 (bidirectional=False) 的高效实现
def forward(x, hx=None):
if batch_first:
x = x.transpose(0, 1)
seq_len, batch_size, _ = x.size()
if hx is None:
hx = torch.zeros(num_layers, batch_size, hidden_size)
h_t_minus_1 = hx
h_t = hx
output = []
for t in range(seq_len):
for layer in range(num_layers):
h_t[layer] = torch.tanh(
x[t] @ weight_ih[layer].T
+ bias_ih[layer]
+ h_t_minus_1[layer] @ weight_hh[layer].T
+ bias_hh[layer]
)
output.append(h_t[-1])
h_t_minus_1 = h_t
output = torch.stack(output)
if batch_first:
output = output.transpose(0, 1)
return output, h_t
Args:
input_size: The number of expected features in the input `x`
hidden_size: The number of features in the hidden state `h`
num_layers: Number of recurrent layers. E.g., setting ``num_layers=2``
would mean stacking two RNNs together to form a `stacked RNN`,
with the second RNN taking in outputs of the first RNN and
computing the final results. Default: 1
nonlinearity: The non-linearity to use. Can be either ``'tanh'`` or ``'relu'``. Default: ``'tanh'``
bias: If ``False``, then the layer does not use bias weights `b_ih` and `b_hh`.
Default: ``True``
batch_first: If ``True``, then the input and output tensors are provided
as `(batch, seq, feature)` instead of `(seq, batch, feature)`.
Note that this does not apply to hidden or cell states. See the
Inputs/Outputs sections below for details. Default: ``False``
dropout: If non-zero, introduces a `Dropout` layer on the outputs of each
RNN layer except the last layer, with dropout probability equal to
:attr:`dropout`. Default: 0
bidirectional: If ``True``, becomes a bidirectional RNN. Default: ``False``
- **`input_size`**:输入 \(x\) 的特征数。
- **`hidden_size`**:隐藏状态 \(h\) 的特征数。
- **`num_layers`**:循环层的数量。例如,设置 `num_layers=2` 表示构成“堆叠的 RNN”,第二层 RNN 会接收第一层 RNN 的输出作为输入,最终输出计算结果。默认值:1。
- **`nonlinearity`**:激活函数,可选择 `"tanh"` 或 `"relu"`。默认值:`"tanh"`。
- **`bias`**:是否使用偏置项 `b_ih` 和 `b_hh`。默认值:`True`。
- **`batch_first`**:若设置为 `True`,输入和输出的张量维度为 `(batch, seq, feature)`;若为 `False`,则为 `(seq, batch, feature)`。隐藏或单元状态维度不受影响。默认值:`False`。
- **`dropout`**:若非零,则对每一层(除最后一层)的输出应用 Dropout,概率为 `dropout`。默认值:`0`。
- **`bidirectional`**:若为 `True`,则为双向 RNN。默认值:`False`。
Inputs: input, hx
* **input**: tensor of shape :math:`(L, H_{in})` for unbatched input,
:math:`(L, N, H_{in})` when ``batch_first=False`` or
:math:`(N, L, H_{in})` when ``batch_first=True`` containing the features of
the input sequence. The input can also be a packed variable length sequence.
See :func:`torch.nn.utils.rnn.pack_padded_sequence` or
:func:`torch.nn.utils.rnn.pack_sequence` for details.
* **hx**: tensor of shape :math:`(D * \text{num\_layers}, H_{out})` for unbatched input or
:math:`(D * \text{num\_layers}, N, H_{out})` containing the initial hidden
state for the input sequence batch. Defaults to zeros if not provided.
where:
.. math::
\begin{aligned}
N ={} & \text{batch size} \\
L ={} & \text{sequence length} \\
D ={} & 2 \text{ if bidirectional=True otherwise } 1 \\
H_{in} ={} & \text{input\_size} \\
H_{out} ={} & \text{hidden\_size}
\end{aligned}
Outputs: output, h_n
* **output**: tensor of shape :math:`(L, D * H_{out})` for unbatched input,
:math:`(L, N, D * H_{out})` when ``batch_first=False`` or
:math:`(N, L, D * H_{out})` when ``batch_first=True`` containing the output features
`(h_t)` from the last layer of the RNN, for each `t`. If a
:class:`torch.nn.utils.rnn.PackedSequence` has been given as the input, the output
will also be a packed sequence.
* **h_n**: tensor of shape :math:`(D * \text{num\_layers}, H_{out})` for unbatched input or
:math:`(D * \text{num\_layers}, N, H_{out})` containing the final hidden state
for each element in the batch.
Attributes:
weight_ih_l[k]: the learnable input-hidden weights of the k-th layer,
of shape `(hidden_size, input_size)` for `k = 0`. Otherwise, the shape is
`(hidden_size, num_directions * hidden_size)`
weight_hh_l[k]: the learnable hidden-hidden weights of the k-th layer,
of shape `(hidden_size, hidden_size)`
bias_ih_l[k]: the learnable input-hidden bias of the k-th layer,
of shape `(hidden_size)`
bias_hh_l[k]: the learnable hidden-hidden bias of the k-th layer,
of shape `(hidden_size)`
.. note::
All the weights and biases are initialized from :math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})`
where :math:`k = \frac{1}{\text{hidden\_size}}`
.. note::
For bidirectional RNNs, forward and backward are directions 0 and 1 respectively.
Example of splitting the output layers when ``batch_first=False``:
``output.view(seq_len, batch, num_directions, hidden_size)``.
.. note::
``batch_first`` argument is ignored for unbatched inputs.
.. include:: ../cudnn_rnn_determinism.rst
.. include:: ../cudnn_persistent_rnn.rst
Examples::
>>> rnn = nn.RNN(10, 20, 2)
>>> input = torch.randn(5, 3, 10)
>>> h0 = torch.randn(2, 3, 20)
>>> output, hn = rnn(input, h0)
"""
@overload
def __init__(
self,
input_size: int,
hidden_size: int,
num_layers: int = 1,
nonlinearity: str = "tanh",
bias: bool = True,
batch_first: bool = False,
dropout: float = 0.0,
bidirectional: bool = False,
device=None,
dtype=None,
) -> None:
...
@overload
def __init__(self, *args, **kwargs):
...
def __init__(self, *args, **kwargs):
if "proj_size" in kwargs:
raise ValueError(
"proj_size argument is only supported for LSTM, not RNN or GRU"
)
if len(args) > 3:
self.nonlinearity = args[3]
args = args[:3] + args[4:]
else:
self.nonlinearity = kwargs.pop("nonlinearity", "tanh")
if self.nonlinearity == "tanh":
mode = "RNN_TANH"
elif self.nonlinearity == "relu":
mode = "RNN_RELU"
else:
raise ValueError(
f"Unknown nonlinearity '{self.nonlinearity}'. Select from 'tanh' or 'relu'."
)
super().__init__(mode, *args, **kwargs)
@overload
@torch._jit_internal._overload_method # noqa: F811
def forward(
self, input: Tensor, hx: Optional[Tensor] = None
) -> tuple[Tensor, Tensor]:
pass
@overload
@torch._jit_internal._overload_method # noqa: F811
def forward(
self, input: PackedSequence, hx: Optional[Tensor] = None
) -> tuple[PackedSequence, Tensor]:
pass
def forward(self, input, hx=None): # noqa: F811
self._update_flat_weights()
num_directions = 2 if self.bidirectional else 1
orig_input = input
if isinstance(orig_input, PackedSequence):
input, batch_sizes, sorted_indices, unsorted_indices = input
max_batch_size = batch_sizes[0]
# script() is unhappy when max_batch_size is different type in cond branches, so we duplicate
if hx is None:
hx = torch.zeros(
self.num_layers * num_directions,
max_batch_size,
self.hidden_size,
dtype=input.dtype,
device=input.device,
)
else:
# Each batch of the hidden state should match the input sequence that
# the user believes he/she is passing in.
hx = self.permute_hidden(hx, sorted_indices)
else:
batch_sizes = None
if input.dim() not in (2, 3):
raise ValueError(
f"RNN: Expected input to be 2D or 3D, got {input.dim()}D tensor instead"
)
is_batched = input.dim() == 3
batch_dim = 0 if self.batch_first else 1
if not is_batched:
input = input.unsqueeze(batch_dim)
if hx is not None:
if hx.dim() != 2:
raise RuntimeError(
f"For unbatched 2-D input, hx should also be 2-D but got {hx.dim()}-D tensor"
)
hx = hx.unsqueeze(1)
else:
if hx is not None and hx.dim() != 3:
raise RuntimeError(
f"For batched 3-D input, hx should also be 3-D but got {hx.dim()}-D tensor"
)
max_batch_size = input.size(0) if self.batch_first else input.size(1)
sorted_indices = None
unsorted_indices = None
if hx is None:
hx = torch.zeros(
self.num_layers * num_directions,
max_batch_size,
self.hidden_size,
dtype=input.dtype,
device=input.device,
)
else:
# Each batch of the hidden state should match the input sequence that
# the user believes he/she is passing in.
hx = self.permute_hidden(hx, sorted_indices)
assert hx is not None
self.check_forward_args(input, hx, batch_sizes)
assert self.mode == "RNN_TANH" or self.mode == "RNN_RELU"
if batch_sizes is None:
if self.mode == "RNN_TANH":
result = _VF.rnn_tanh(
input,
hx,
self._flat_weights, # type: ignore[arg-type]
self.bias,
self.num_layers,
self.dropout,
self.training,
self.bidirectional,
self.batch_first,
)
else:
result = _VF.rnn_relu(
input,
hx,
self._flat_weights, # type: ignore[arg-type]
self.bias,
self.num_layers,
self.dropout,
self.training,
self.bidirectional,
self.batch_first,
)
else:
if self.mode == "RNN_TANH":
result = _VF.rnn_tanh(
input,
batch_sizes,
hx,
self._flat_weights, # type: ignore[arg-type]
self.bias,
self.num_layers,
self.dropout,
self.training,
self.bidirectional,
)
else:
result = _VF.rnn_relu(
input,
batch_sizes,
hx,
self._flat_weights, # type: ignore[arg-type]
self.bias,
self.num_layers,
self.dropout,
self.training,
self.bidirectional,
)
output = result[0]
hidden = result[1]
if isinstance(orig_input, PackedSequence):
output_packed = PackedSequence(
output, batch_sizes, sorted_indices, unsorted_indices
)
return output_packed, self.permute_hidden(hidden, unsorted_indices)
if not is_batched: # type: ignore[possibly-undefined]
output = output.squeeze(batch_dim) # type: ignore[possibly-undefined]
hidden = hidden.squeeze(1)
return output, self.permute_hidden(hidden, unsorted_indices)
# XXX: LSTM and GRU implementation is different from RNNBase, this is because:
# 1. we want to support nn.LSTM and nn.GRU in TorchScript and TorchScript in
# its current state could not support the python Union Type or Any Type
# 我们希望支持 nn.LSTM 和 nn.GRU 在 TorchScript 中,但当前状态下,TorchScript 无法支持 Python 的 Union 类型或 Any 类型。
# 2. TorchScript static typing does not allow a Function or Callable type in
# Dict values, so we have to separately call _VF instead of using _rnn_impls
# TorchScript 的静态类型检查不允许在字典的值中使用函数或可调用类型,因此我们必须单独调用 _VF,而不能使用 _rnn_impls。
# 3. This is temporary only and in the transition state that we want to make it
# on time for the release
# 这只是临时的,目前处于过渡阶段,我们希望能够按时发布。
# More discussion details in https://github.com/pytorch/pytorch/pull/23266
#
# TODO: remove the overriding implementations for LSTM and GRU when TorchScript
# support expressing these two modules generally.
# TODO:当 TorchScript 支持一般性地表达这两个模块时,移除 LSTM 和 GRU 的覆盖实现。