Adam

ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION

解决了什么问题

基于传统随机梯度下降算法的一阶优化算法

贡献点

1. 结合了AdaGrad(自适应梯度算法)和RMSProp(均方根传播算法)两种梯度优化算法的优点

优势

1. 实现简单，计算高效，对内存需求少

2. 参数的更新不受梯度的伸缩变换影响

3. 超参数具有很好的解释性，且通常无需调整或仅需很少的微调

4. 更新的步长能够被限制在大致的范围内（初始学习率）

5. 能自然地实现步长退火过程（自动调整学习率）

6. 很适合应用于大规模的数据及参数的场景

7. 适用于不稳定目标函数

8. 适用于梯度稀疏或梯度存在很大噪声的问题

缺点

1. 在某些极端情况下不会收敛到最优值
2. Adam 可能会遇到权重衰减问题

方法

参数:

A	B	C
1	\(m_{t}\)	一阶矩向量(the mean)
2	\(v_{t}\)	二阶矩向量(the uncentered variance)
3	t	迭代数
4	\(\theta_{t}\)	参数向量
5	\(f_{t}(\theta)\)	随机目标函数
6	\(g_{t}\)	梯度
7	\(\beta_{1},\beta_{2}\)	矩估计的指数衰减率
8	\(\alpha\)	步长, 算法中通过\(\alpha_{t} = \frac{\alpha}{1-\beta_{1}^{t}}\)更新
9	\(\hat{m_{t}}\)	偏差修正的一阶矩估计
10	\(\hat{v_{t}}\)	偏差修正的二阶原始矩估计

数据集

1. MNIST
2. IMDb Movie Reviews
3. CIFAR10

效果

1. LOGISTIC REGRESSION
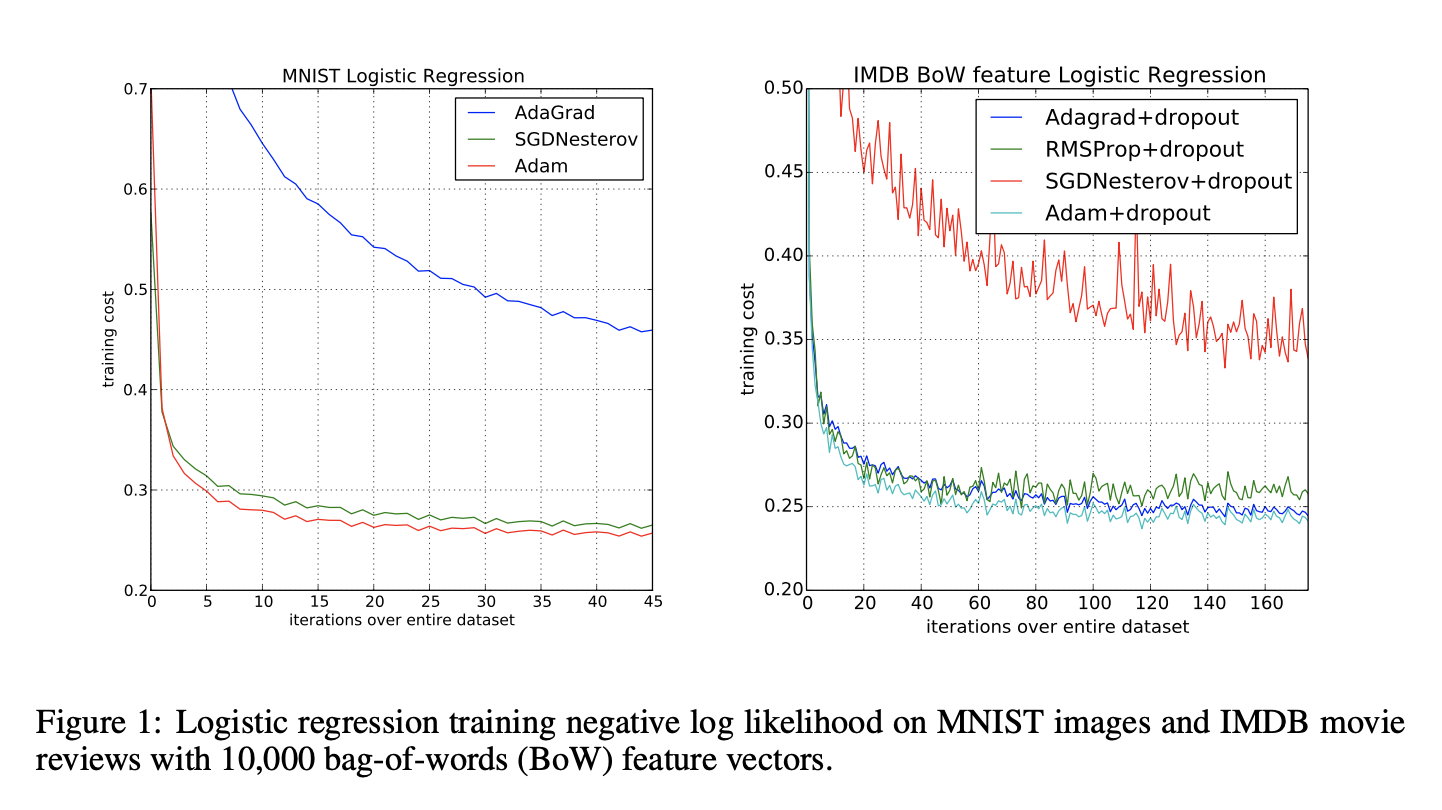
2. MULTI-LAYER NEURAL NETWORKS
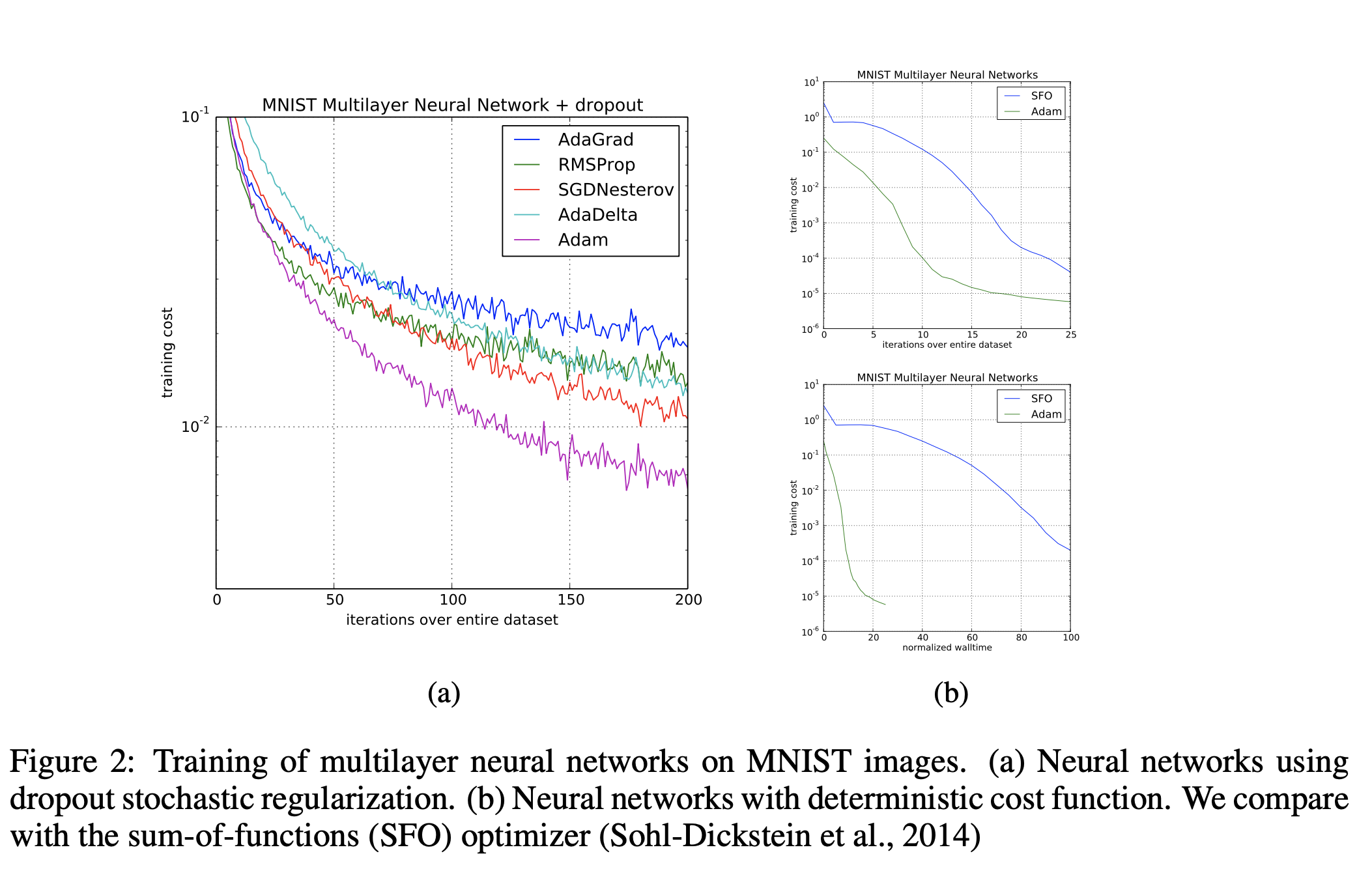
3. CONVOLUTIONAL NEURAL NETWORKS
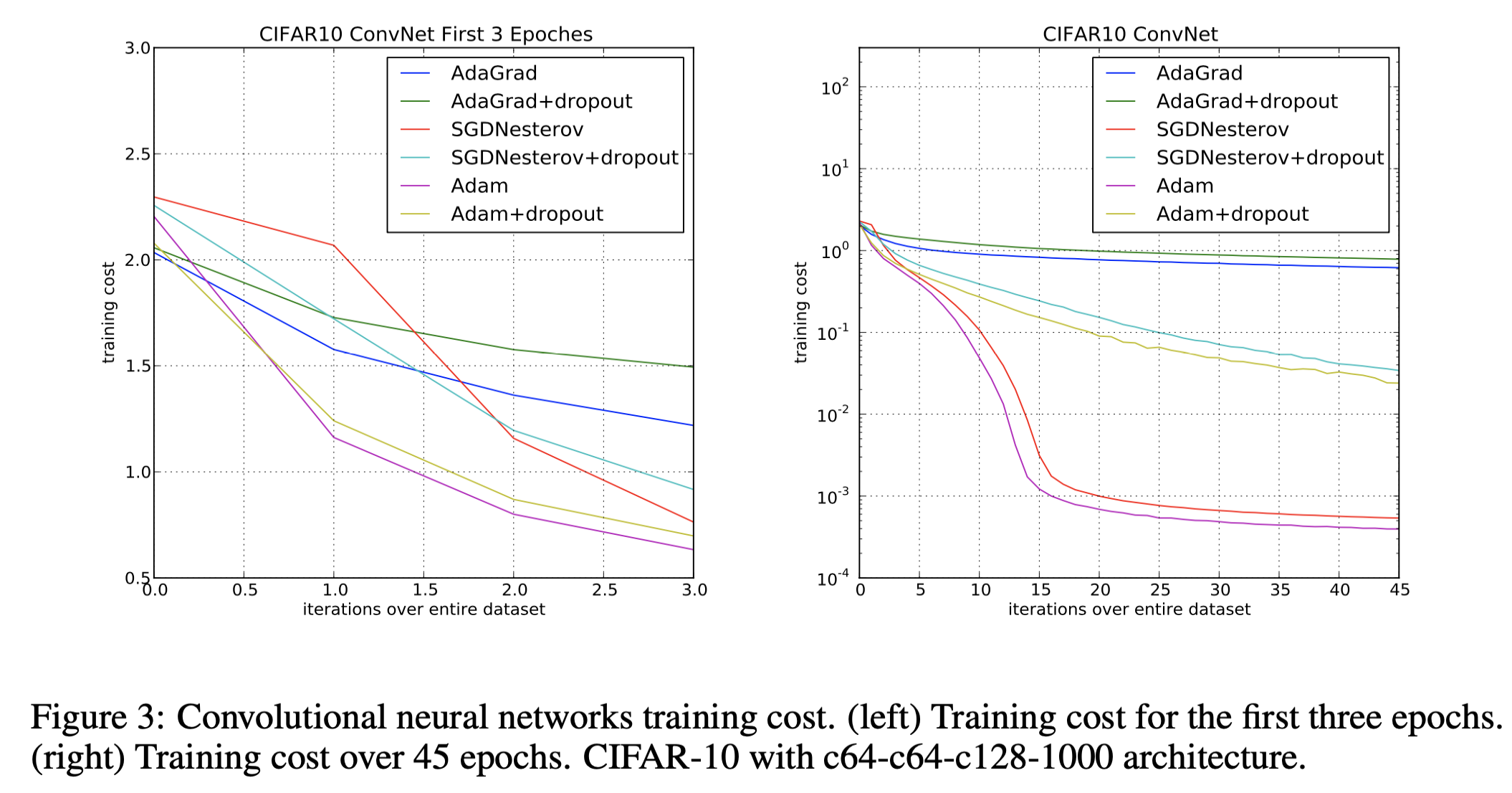
4. BIAS-CORRECTION TERM

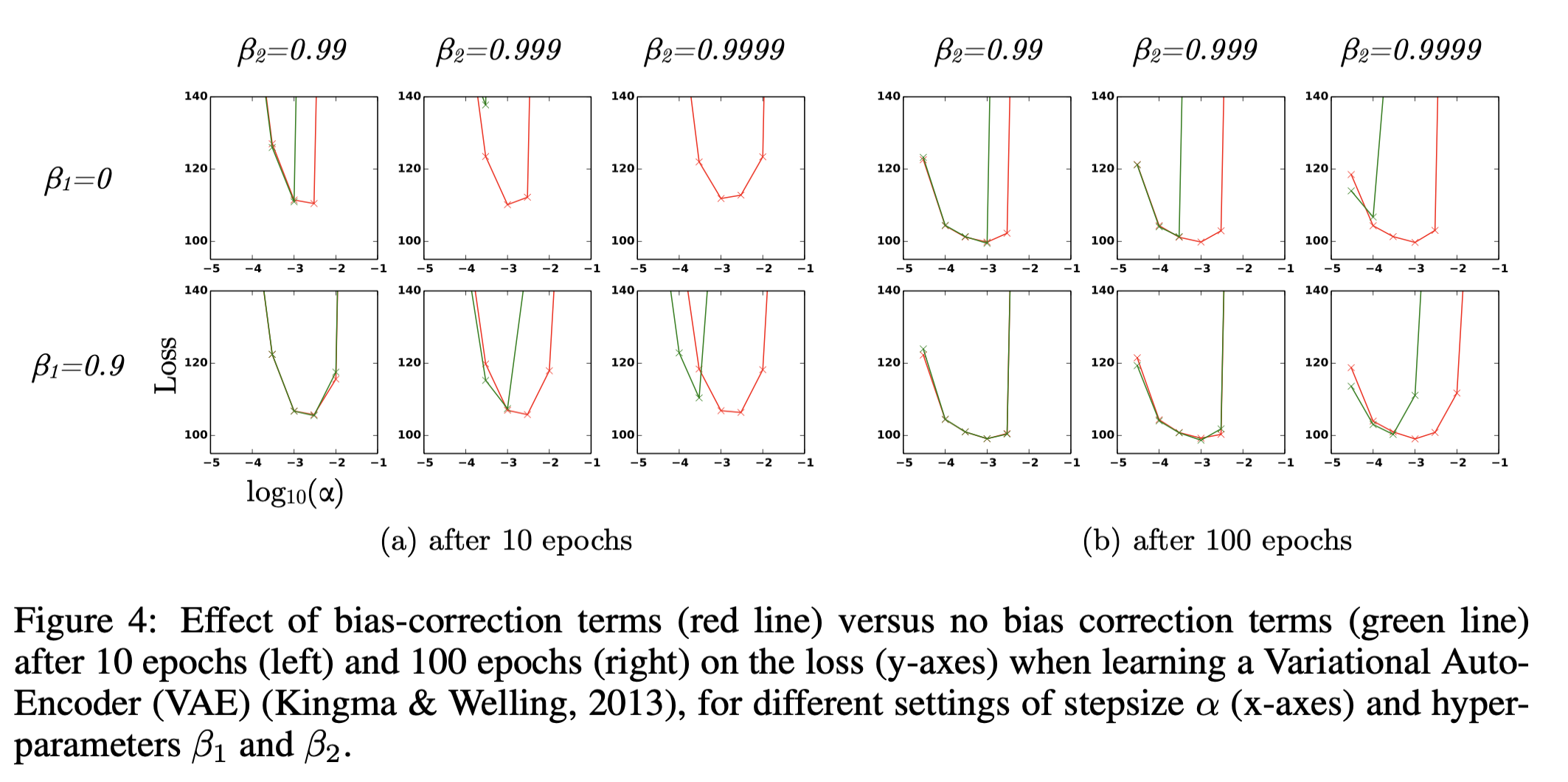
收敛性证明

当\(f_{t}(\theta)\) 为convex函数时，判定指标选择为统计量R(T)（Regret）：

\[R(T) = \sum_{i=1}^{T} [f_{t}(\theta_{t}) − f_{t}(\theta^{*})]\]

其中 \(\theta^{*} = arg min_{\theta \in \chi}\sum_{i=1}^{T} f_{t}(\theta)\)

方法: 求取 R(T) 的一个上界，然后利用上界值除以 T 在极限情况下是否趋于0来判定收敛性。

\[\frac{R(T)}{T} =O(\frac{1}{\sqrt{T}})\]

假设:

1. \(g_{t} \triangleq \nabla f_{t}(\theta_{t})\),其中\(i \in \mathbb{R}^{t}\)表示第i维从1到t的梯度向量,表示为\(g_{1:t,i}=[g_{1,i},g_{2,i} \dots g_{t,i}]\)
2. \[\gamma \triangleq \frac{\beta_{1}^{2}}{\sqrt{\beta_{2}}} < 1, \beta_{1},\beta_{2} \in [0,1)\]
3. \[\beta_{1,t}=\beta_{1} \cdot \lambda^{t-1},\lambda \in (0,1) \Rightarrow \beta_{1,t} \le \beta_{1}\]
4. \[\alpha_{t}=\frac{\alpha}{\sqrt{t}}\]

平均不等式:

\[\begin{eqnarray} \forall &x_{1}&,x_{2} \dots x_{n} \in \mathbb{N}, \\ &0&<{\frac {n}{1/x_{1}+1/x_{2}+\cdots +1/x_{n}}} \leq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}\leq {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\leq {\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}}{n}}}\\ \Rightarrow &0&<\cfrac {n}{\sum_{i=1}^{n} \cfrac{1}{x_{i}}} \leq \sqrt[{n}]{\prod_{i=1}^{n}x_{i} } \leq \frac{\sum_{i=1}^{n}x_{i}}{n} \le \sqrt[]{\frac{\sum_{i=1}^{n}x_{i}^{2}}{n} } \tag{0} \end{eqnarray}\]

根据定义, 如果f是一个凸函数, 则对于所有的\(x,y \in \mathbb{R}^{d}, \lambda \in [0,1]\)都有 \(\begin{eqnarray} \lambda f(x)+(1-\lambda)f(y) \ge f(\lambda x+(1-\lambda)y) \tag{1} \\ \Rightarrow f(y) \ge f(x) + \nabla f(x)^{T} (y − x) \tag{2} \end{eqnarray}\)

由(2)式可得,

\[\begin{align*} &f_{t}(\mathbf{\theta}^{\ast} ) \ge f_{t}(\mathbf{\theta}_{t})+g_{t}^{T} \cdot (\mathbf{\theta}^{\ast} - \mathbf{\theta}_{t})\\ \Rightarrow &f_{t}(\mathbf{\theta}_{t}) - f_{t}(\mathbf{\theta}^{\ast} ) \le g_{t}^{T} \cdot (\mathbf{\theta}_{t} - \mathbf{\theta}^{\ast})\\ \Rightarrow &R(T) \le \sum_{t = 1}^{T} \langle g_{t}^{T} ,\mathbf{\theta}_{t} - \mathbf{\theta}^{\ast} \rangle = \sum_{i = 1}^{d}\sum_{t = 1}^{T} \langle g_{t,i} ,\mathbf{\theta}_{t,i} - \theta_{,i}^{\ast} \rangle \tag{3}\\ \end{align*}\]

对于算法1更新参数:

\[\begin{eqnarray} \theta_{t+1} & = & \theta_{t} - \alpha_{t} \cdot \frac{\hat{m}_{t}}{\sqrt{\hat{v_{t}}}}\\ & = & \theta_{t} - \frac{\alpha_{t}}{1-\beta_{1}^{t}}(\frac{\beta_{1,t}m_{t-1}+(1-\beta_{1,t})g_{t}}{\sqrt{\hat{v_{t}}}}) \end{eqnarray}\]

对两边减去参数theta然后平方可得:

\[\begin{eqnarray} (\theta_{t+1,i} - \theta_{,i}^{\ast})^{2} & = & (\theta_{t,i} - \theta_{,i}^{\ast} - \alpha_{t} \cdot \frac{\hat{m}_{t,i}}{\sqrt{\hat{v_{t,i}}}})^{2}\\ & = & (\theta_{t,i} - \theta_{,i}^{\ast})^{2} + (\alpha_{t}\frac{\hat{m}_{t,i}}{\sqrt{\hat{v_{t,i}}}})^{2} - 2\alpha_{t}\frac{\hat{m}_{t,i}}{\sqrt{\hat{v_{t,i}}}}(\theta_{t,i} - \theta_{,i}^{\ast})\\ & = & (\theta_{t,i} - \theta_{,i}^{\ast})^{2} + (\alpha_{t}\frac{\hat{m}_{t,i}}{\sqrt{\hat{v_{t,i}}}})^{2} - \frac{2\alpha_{t}}{1-\beta_{1}^{t}}(\frac{\beta_{1,t}m_{t-1}+(1-\beta_{1,t})g_{t,i}}{\sqrt{\hat{v_{t,i}}}})(\theta_{t,i} - \theta_{,i}^{\ast}) \end{eqnarray}\]

对上式进行分离缩放:

\[\begin{eqnarray} \Rightarrow g_{t,i}(\theta_{t,i} - \theta_{,i}^{\ast}) & = & \cfrac{\sqrt{\hat{v}_{t,i} } \cdot \cfrac{-(1-\beta_{1}^{t}){\Large(}(\theta_{t+1,i} - \theta_{,i}^{\ast})^{2}-(\theta_{t,i} - \theta_{,i}^{\ast})^{2}-(\alpha_{t}\frac{\hat{m_{t,i}}}{\sqrt{\hat{v_{t,i}}}})^{2}{\Large)}}{2\alpha_{t}} - \beta_{1,t}m_{t-1,i}(\theta_{t,i} - \theta_{,i}^{\ast})}{1- \beta_{1,t}}\\ & = & \frac{-\sqrt{\hat{v}_{t,i}}(1-\beta_{1}^{t}){\Large(}(\theta_{t+1,i} - \theta_{,i}^{\ast})^{2}-(\theta_{t,i} - \theta_{,i}^{\ast})^{2}-(\alpha_{t}\frac{\hat{m_{t,i}}}{\sqrt{\hat{v_{t,i}}}})^{2}{\Large)}}{2\alpha_{t}(1- \beta_{1,t})} - \frac{\beta_{1,t}m_{t-1,i}(\theta_{t,i} - \theta_{,i}^{\ast})}{1- \beta_{1,t}} \\ & = & \frac{\sqrt{\hat{v}_{t,i}}(1-\beta_{1}^{t}){\Large(}(\theta_{t,i} - \theta_{,i}^{\ast})^{2}-(\theta_{t+1,i} - \theta_{,i}^{\ast})^{2}{\Large)}}{2\alpha_{t}(1- \beta_{1,t})}+\frac{\alpha_{t}\sqrt{\hat{v}_{t,i}}(1-\beta_{1}^{t})}{2(1- \beta_{1,t})} (\frac{\hat{m_{t,i}}}{\sqrt{\hat{v_{t,i}}}})^{2} - \frac{\beta_{1,t}m_{t-1,i}(\theta_{t,i} - \theta_{,i}^{\ast})}{1- \beta_{1,t}} \\ & = & \frac{\sqrt{\hat{v}_{t,i}}(1-\beta_{1}^{t}){\Large(}(\theta_{t,i} - \theta_{,i}^{\ast})^{2}-(\theta_{t+1,i} - \theta_{,i}^{\ast})^{2}{\Large)}}{2\alpha_{t}(1- \beta_{1,t})}+\frac{\alpha_{t}\sqrt{\hat{v}_{t,i}}(1-\beta_{1}^{t})}{2(1- \beta_{1,t})} (\frac{\hat{m_{t,i}}}{\sqrt{\hat{v_{t,i}}}})^{2} + \frac{\beta_{1,t}m_{t-1,i}(\theta_{,i}^{\ast} - \theta_{t,i})\frac{\hat{v}_{t-1,i}^{\frac{1}{4}}}{\sqrt{\alpha_{t-1}}} \frac{\sqrt{\alpha_{t-1}}}{\hat{v}_{t-1,i}^{\frac{1}{4}}} } {1- \beta_{1,t}} \\ & \le & \frac{\sqrt{\hat{v}_{t,i}}{\Large(}(\theta_{t,i} - \theta_{,i}^{\ast})^{2}-(\theta_{t+1,i} - \theta_{,i}^{\ast})^{2}{\Large)}}{2\alpha_{t}(1- \beta_{1,t})}+\frac{\alpha_{t}}{2(1- \beta_{1,t})} \frac{\hat{m}_{t,i}^{2}}{\sqrt{\hat{v_{t,i}}}} + \frac{\beta_{1,t}(\theta_{,i}^{\ast} - \theta_{t,i})\frac{\hat{v}_{t-1,i}^{\frac{1}{4}}}{\sqrt{\alpha_{t-1}}} m_{t-1,i}\frac{\sqrt{\alpha_{t-1}}}{\hat{v}_{t-1,i}^{\frac{1}{4}}} } {1- \beta_{1,t}} \\ & \le & \frac{\sqrt{\hat{v}_{t,i}}{\Large(}(\theta_{t,i} - \theta_{,i}^{\ast})^{2}-(\theta_{t+1,i} - \theta_{,i}^{\ast})^{2}{\Large)}}{2\alpha_{t}(1- \beta_{1,t})}+\frac{\alpha_{t}}{2(1- \beta_{1,t})} \frac{\hat{m}_{t,i}^{2}}{\sqrt{\hat{v_{t,i}}}} + \frac{\beta_{1,t}\sqrt{\hat{v}_{t-1,i}} }{2\alpha_{t-1}(1- \beta_{1,t})}(\theta_{,i}^{\ast} - \theta_{t,i})^{2} + \frac{\beta_{1,t}m_{t-1,i}^{2}\alpha_{t-1}}{2 (1- \beta_{1,t}) \sqrt{\hat{v}_{t-1,i}} } \tag{4}\\ \end{eqnarray}\]

注释: 根据杨氏不等式\(ab \le \frac{a^{2}}{2} + \frac{b^{2}}{2}\),

其中

\[\begin{eqnarray} a & = & (\theta_{,i}^{\ast} - \theta_{t,i})\frac{\hat{v}_{t-1,i}^{\frac{1}{4}}}{\sqrt{\alpha_{t-1}}}\\ b & = & m_{t-1,i}\frac{\sqrt{\alpha_{t-1}}}{\hat{v}_{t-1,i}^{\frac{1}{4}}} \end{eqnarray}\]

把(4)式带入(3)式可得,

\[\begin{eqnarray} R(T) &\le& \sum_{i=1}^{d}\sum_{t=1}^{T} {\Large [ }\frac{\sqrt{\hat{v}_{t,i}}{\Large(}(\theta_{t,i} - \theta_{,i}^{\ast})^{2}-(\theta_{t+1,i} - \theta_{,i}^{\ast})^{2}{\Large)}}{2\alpha_{t}(1- \beta_{1,t})}+\frac{\alpha_{t}}{2(1- \beta_{1,t})} \frac{\hat{m}_{t,i}^{2}}{\sqrt{\hat{v_{t,i}}}} + \frac{\beta_{1,t}\sqrt{\hat{v}_{t-1,i}} }{2\alpha_{t-1}(1- \beta_{1,t})}(\theta_{,i}^{\ast} - \theta_{t-1,i})^{2} + \frac{\beta_{1,t}m_{t-1,i}^{2}\alpha_{t-1}}{2 (1- \beta_{1,t}) \sqrt{\hat{v}_{t-1,i}} }{\Large ]}\\ \end{eqnarray}\]

其中

\[\begin{eqnarray} \sum_{t = 1}^{T} \frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} \le \frac{2}{1-\gamma} \frac{G_{\infty}}{\sqrt{1-\beta_{2}}}\left \| g_{1:T,i} \right \|_{2} \tag{5} \end{eqnarray}\]

证明:

假设: \(\frac{\sqrt{(1-\beta_{2}^{t})}}{(1-\beta_{1}^{t})^{2}} \le \frac{1}{(1-\beta_{1})^{2}} \tag{6}\)

参数有界:

\[\begin{eqnarray} \left \| \theta_{n} - \theta_{m} \right \|_{2} &\le& D\\ \left \| \theta_{n} - \theta_{m} \right \|_{\infty} &\le& D_{\infty} \tag{7} \end{eqnarray}\]

其中,

\[\begin{eqnarray} \sqrt{\hat{v}_{t,i}} & = & \frac{\sqrt{\sum_{j = 1}^{t}(1-\beta_{2})\beta_{2}^{t-j}g_{j,i}^{2}}}{\sqrt{1-\beta_{2}^{t}}} \le \left \| g_{1:t,i} \right \|_{2} \tag{8}\\ \hat{m}_{t,i}^{2} & = & \frac{(\beta_{1}m_{t-1,i}+(1-\beta_{1})g_{t,i})^{2}}{(1-\beta_{1}^{t})^{2}} \\ & = & \frac{(\sum_{k=1}^{t} \beta_{1}^{t-k}(1-\beta_{1})g_{k,i})^{2}}{(1-\beta_{1}^{t})^{2}} \le \left \| g_{1:t,i} \right \|_{2}^{2} \tag{9} \end{eqnarray}\]

展开不等式(5)左边的最后一项:

\[\begin{eqnarray} \sum_{t = 1}^{T} \frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} & = & \sum_{t = 1}^{T-1}\frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} + \frac{\hat{m}_{T,i}^{2}}{\sqrt{T \hat{v}_{T,i}}}\\ & = & \sum_{t = 1}^{T-1}\frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} + \cfrac{\cfrac{m_{T,i}^{2}}{(1-\beta_{1}^{T})^{2}} }{\sqrt{T \cfrac{v_{T,i}}{1-\beta_{2}^{T}} }}\\ & = & \sum_{t = 1}^{T-1}\frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} + \cfrac{\cfrac{(\beta_{1}m_{T-1,i}+(1-\beta_{1})g_{T,i})^{2}}{(1-\beta_{1}^{T})^{2}} }{\sqrt{T \cfrac{\beta_{2}v_{T-1,i}+(1-\beta_{2})g_{T,i}^{2}}{1-\beta_{2}^{T}} }}\\ & = & \sum_{t = 1}^{T-1}\frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} + \frac{\sqrt{1-\beta_{2}^{T}} }{(1-\beta_{1}^{T})^{2}} \frac{(\sum_{k=1}^{T}(1-\beta_{1})\beta_{1}^{T-k}g_{k,i})^{2}}{\sqrt{T \sum_{j=1}^{T}(1-\beta_{2})\beta_{2}^{T-j}g_{j,i}^{2}} } \\ & \le & \sum_{t = 1}^{T-1}\frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} + \frac{\sqrt{1-\beta_{2}^{T}} }{(1-\beta_{1}^{T})^{2}} \sum_{k=1}^{T} \frac{T((1-\beta_{1})\beta_{1}^{T-k}g_{k,i})^{2}}{\sqrt{T \sum_{j=1}^{T}(1-\beta_{2})\beta_{2}^{T-j}g_{j,i}^{2}}} \tag{根据平均不等式(0)}\\ & \le & \sum_{t = 1}^{T-1}\frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} + \frac{\sqrt{1-\beta_{2}^{T}} }{(1-\beta_{1}^{T})^{2}} \sum_{k=1}^{T} \frac{T((1-\beta_{1})\beta_{1}^{T-k}g_{k,i})^{2}}{\sqrt{T (1-\beta_{2})\beta_{2}^{T-k}g_{k,i}^{2}}}\\ & \le & \sum_{t = 1}^{T-1}\frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} + \frac{\sqrt{1-\beta_{2}^{T}} }{(1-\beta_{1}^{T})^{2}} \frac{(1-\beta_{1})^{2}}{\sqrt{T(1-\beta_{2})} } \sum_{k=1}^{T} T (\frac{\beta_{1}^{2}}{\sqrt{\beta_{2}}})^{T-k}\left \| g_{k,i} \right \|_{2}\\ & \le & \sum_{t = 1}^{T-1}\frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} + \frac{T}{\sqrt{T(1-\beta_{2})} } \sum_{k=1}^{T} \gamma^{T-k}\left \| g_{k,i} \right \|_{2} \tag{带入不等式(6)和假设2}\\ \Rightarrow \sum_{t = 1}^{T} \frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} & \le & \sum_{t=1}^{T} \frac{\left \| g_{t,i} \right \|_{2} }{\sqrt{t(1-\beta_{2})} } \sum_{j=0}^{T-t} t \gamma^{j}\\ & \le & \sum_{t=1}^{T} \frac{\left \| g_{t,i} \right \|_{2} }{\sqrt{t(1-\beta_{2})}} \sum_{j=0}^{T} t \gamma^{j} \tag{10} \end{eqnarray}\]

根据等比数列求和公式:

\[\begin{eqnarray} S_{n} & = & {\frac {a(1-r^{n})}{1-r}}, \forall r \ne 1 \\ \Rightarrow S_{\infty} & = & \frac{a}{1-r} ,\forall -1 < r <1\\ \sum_{j=0}^{T} t \gamma^{j} & = & t \cdot \frac{1-\gamma^{T}}{1-\gamma} < \frac{t}{1-\gamma} \tag{11} \\ \end{eqnarray}\]

把(11)式带入(10)式得,

\[\begin{eqnarray} \sum_{t=1}^{T} \frac{\left \| g_{t,i} \right \|_{2} }{\sqrt[]{t(1-\beta_{2})} } \sum_{j=0}^{T} t \gamma^{j} \le \frac{1}{(1-\gamma)\sqrt{1-\beta_{2}} } \sum_{t=1}^{T} \frac{\left \| g_{t,i} \right \|_{2}}{\sqrt{t} } \tag{12} \end{eqnarray}\]

梯度有界:

\[\begin{eqnarray} \left \| g_{t} \right \|_{2} \le G,\left \| g_{t} \right \|_{\infty} \le G_{\infty} \Rightarrow \sum_{t = 1}^{T} \sqrt{\frac{g_{t,i}^{2}}{t}} \le 2G_{\infty}\left \| g_{1:T,i} \right \|_{2} \tag{13} \end{eqnarray}\]

运用数学归纳法证明:

当T=1时, \(\sqrt{g_{1,i}^{2}} \le 2G_{\infty} \left \| g_{1:T,i} \right \|_{2}\)
当T=T时, \(\begin{eqnarray} \sum_{t=1}^{T} \sqrt{\frac{g_{t,i}^{2}}{t}} & = & \sum_{t=1}^{T-1} \sqrt{\frac{g_{t,i}^{2}}{t}} + \sqrt{\frac{g_{T,i}^{2}}{T}}\\ &\le& 2G_{\infty} \left \| g_{1:T-1,i} \right \|_{2} + \sqrt{\frac{g_{T,i}^{2}}{T}}\\ &=&2G_{\infty} \sqrt{\left \|g_{1:T,i} \right \|_{2}^{2}-g_{T}^{2}} + \sqrt{\frac{g_{T,i}^{2}}{T}} \tag{14} \end{eqnarray}\)

设 \(\left \|g_{1:T,i} \right \|_{2}^{2}-g_{T}^{2} + \frac{g_{T,i}^{4}}{4\left \| g_{1:T,i} \right \|_{2}^{2}} \ge \left \|g_{1:T,i} \right \|_{2}^{2}-g_{T}^{2}\)

两边开根号得,

\[\begin{eqnarray} \Rightarrow \sqrt{\left \|g_{1:T,i} \right \|_{2}^{2}-g_{T}^{2}} &\le& \left \|g_{1:T,i} \right \|_{2} - \frac{g_{T,i}^{2}}{2\left \| g_{1:T,i} \right \|_{2}}\\ &\le&\left \|g_{1:T,i} \right \|_{2} - \frac{g_{T,i}^{2}}{2\sqrt{TG_{\infty}^{2}} } \end{eqnarray}\]

对不等号左边换算成公式(14):

\[\begin{eqnarray} G_{\infty}\sqrt{\left \|g_{1:T,i} \right \|_{2}^{2}-g_{T}^{2}} &\le& G_{\infty}\left \|g_{1:T,i} \right \|_{2} - \frac{g_{T,i}^{2}}{2\sqrt{T} }\\ 2G_{\infty}\sqrt{\left \|g_{1:T,i} \right \|_{2}^{2}-g_{T}^{2}} &\le& 2G_{\infty}\left \|g_{1:T,i} \right \|_{2} - \frac{g_{T,i}^{2}}{\sqrt{T} }\\ 2G_{\infty}\sqrt{\left \|g_{1:T,i} \right \|_{2}^{2}-g_{T}^{2}} + \sqrt{\frac{g_{T,i}^{2}}{T}} &\le& 2G_{\infty}\left \|g_{1:T,i} \right \|_{2} - \frac{g_{T,i}^{2}}{\sqrt{T} } + \sqrt{\frac{g_{T,i}^{2}}{T}}\\ 2G_{\infty}\sqrt{\left \|g_{1:T,i} \right \|_{2}^{2}-g_{T}^{2}} + \sqrt{\frac{g_{T,i}^{2}}{T}} &\le& 2G_{\infty}\left \|g_{1:T,i} \right \|_{2} - \frac{g_{T,i}^{2}-g_{T,i}}{\sqrt{T}} \le 2G_{\infty}\left \|g_{1:T,i} \right \|_{2} \\ \Rightarrow \sum_{t = 1}^{T} \sqrt{\frac{g_{t,i}^{2}}{t}} &\le& 2G_{\infty}\left \| g_{1:T,i} \right \|_{2} \end{eqnarray}\]

把公式(11)带入公式(10)得,

\[\begin{eqnarray} \sum_{t = 1}^{T} \frac{\hat{m}_{t,i}^{2}}{\sqrt{t \hat{v}_{t,i}}} \le \frac{2G_{\infty}}{(1-\gamma)\sqrt{1-\beta_{2}} } \left \| g_{1:T,i} \right \|_{2} \tag{15} \end{eqnarray}\]

所以,

\[\begin{eqnarray} R(T) &\le& \sum_{i=1}^{d}\sum_{t=1}^{T} {\Large [ }\frac{\sqrt{\hat{v}_{t,i}}{\Large(}(\theta_{t,i} - \theta_{,i}^{\ast})^{2}-(\theta_{t+1,i} - \theta_{,i}^{\ast})^{2}{\Large)}}{2\alpha_{t}(1- \beta_{1,t})} + \frac{\alpha_{t}}{2(1- \beta_{1,t})} \frac{\hat{m}_{t,i}^{2}}{\sqrt{\hat{v_{t,i}}}} + \frac{\beta_{1,t}\sqrt{\hat{v}_{t-1,i}} }{2\alpha_{t-1}(1- \beta_{1,t})}(\theta_{,i}^{\ast} - \theta_{t,i})^{2} + \frac{\beta_{1,t}m_{t-1,i}^{2}\alpha_{t-1}}{2 (1- \beta_{1,t}) \sqrt{\hat{v}_{t-1,i}} }{\Large ]}\\ &\le& \sum_{i=1}^{d}\sum_{t=1}^{T}[\frac{\sqrt{\hat{v}_{t,i}}(\theta_{t,i} - \theta_{,i}^{\ast})^{2}}{2\alpha_{t}(1- \beta_{1,t})} - \frac{\sqrt{\hat{v}_{t,i}}(\theta_{t+1,i} - \theta_{,i}^{\ast})^{2}}{2\alpha_{t}(1- \beta_{1,t})} + \frac{\beta_{1,t}\sqrt{\hat{v}_{t-1,i}} }{2\alpha_{t-1}(1- \beta_{1,t})}(\theta_{,i}^{\ast} - \theta_{t,i})^{2} + \frac{\alpha_{t}}{2(1- \beta_{1,t})} \frac{\hat{m}_{t,i}^{2}}{\sqrt{\hat{v_{t,i}}}} +\frac{\beta_{1,t}m_{t-1,i}^{2}\alpha_{t-1}}{2 (1- \beta_{1,t}) \sqrt{\hat{v}_{t-1,i}} }] \\ &\le& \sum_{i=1}^{d} [\frac{\sqrt{\hat{v}_{1,i}}(\theta_{1,i} - \theta_{,i}^{\ast})^{2}}{2\alpha_{1}(1- \beta_{1,1})} - \frac{\sqrt{\hat{v}_{T,i}}(\theta_{T+1,i} - \theta_{,i}^{\ast})^{2}}{2\alpha_{T}(1- \beta_{1,T})}] + \sum_{i=1}^{d}\sum_{t=2}^{T}[\frac{\sqrt{\hat{v}_{t,i}}(\theta_{t,i} - \theta_{,i}^{\ast})^{2}}{2\alpha_{t}(1- \beta_{1,t})} - \frac{\sqrt{\hat{v}_{t-1,i}}(\theta_{t,i} - \theta_{,i}^{\ast})^{2}}{2\alpha_{t-1}(1- \beta_{1,t-1})} ] + \sum_{i=1}^{d}\sum_{t=1}^{T} [\frac{\beta_{1,t}\sqrt{\hat{v}_{t-1,i}} }{2\alpha_{t-1}(1- \beta_{1,t})}(\theta_{,i}^{\ast}- \theta_{t,i})^{2} + \frac{\alpha_{t}}{2(1- \beta_{1,t})} \frac{\hat{m}_{t,i}^{2}}{\sqrt{\hat{v_{t,i}}}} +\frac{\beta_{1,t}\alpha_{t-1}}{2 (1- \beta_{1,t}) }\frac{m_{t-1,i}^{2}}{\sqrt{\hat{v}_{t-1,i}}} ] \\ &\le& \sum_{i=1}^{d} [\frac{\sqrt{\hat{v}_{1,i}}(\theta_{1,i} - \theta_{,i}^{\ast})^{2}}{2\alpha_{1}(1- \beta_{1,1})} - \frac{\sqrt{\hat{v}_{T,i}}(\theta_{T+1,i} - \theta_{,i}^{\ast})^{2}}{2\alpha_{T}(1- \beta_{1,T})}] + \frac{1}{2(1-\beta_{1})} \sum_{i=1}^{d}\sum_{t=2}^{T} (\theta_{t,i} - \theta_{,i}^{\ast})^{2}(\frac{\sqrt{\hat{v}_{t,i}}}{\alpha_{t}} - \frac{\sqrt{\hat{v}_{t-1,i}}}{\alpha_{t-1}} ) + \sum_{i=1}^{d}\sum_{t=1}^{T} [\frac{\beta_{1,t}\sqrt{\hat{v}_{t-1,i}} }{2\alpha_{t-1}(1- \beta_{1,t})}(\theta_{,i}^{\ast}- \theta_{t,i})^{2}] + \frac{\alpha}{2(1-\beta_{1})}\frac{2G_{\infty}}{(1-\gamma)\sqrt{1-\beta_{2}} } \sum_{i = 1}^{d}\left \| g_{1:T,i} \right \|_{2}+\frac{\alpha \beta_{1}}{2(1-\beta_{1})}\frac{2G_{\infty}}{(1-\gamma)\sqrt{1-\beta_{2}} } \sum_{i = 1}^{d}\left \| g_{1:T,i} \right \|_{2} \tag{把(12)式和假设4带入}\\ &\le& \sum_{i=1}^{d} [\frac{\sqrt{\hat{v}_{1,i}}D^{2}}{2\alpha_{1}(1- \beta_{1,1})} - \frac{\sqrt{\hat{v}_{T,i}}D^{2}}{2\alpha_{T}(1- \beta_{1,T})}] + \frac{D_{\infty}^{2}}{2\alpha_{1}(1-\beta_{1})} \sum_{i=1}^{d}\sum_{t=2}^{T} (\sqrt{t\hat{v}_{t,i}} - \sqrt{(t-1)\hat{v}_{t-1,i}} ) + \frac{D_{\infty}^{2}}{2\alpha_{1}} \sum_{i=1}^{d} [\frac{\beta_{1,t}\sqrt{(t-1)\hat{v}_{t-1,i}} }{(1- \beta_{1,t})}] + \frac{\alpha_{1}(1+\beta_{1})}{(1-\beta_{1})}\frac{G_{\infty}}{(1-\gamma)\sqrt{1-\beta_{2}} } \sum_{i = 1}^{d}\left \| g_{1:T,i} \right \|_{2}\tag{带入公式(7)}\\ &\le& \sum_{i=1}^{d} [\frac{\sqrt{\hat{v}_{1,i}}D^{2}}{2\alpha_{1}(1- \beta_{1,1})} - \frac{\sqrt{\hat{v}_{T,i}}D^{2}}{2\alpha_{T}(1- \beta_{1,T})}] + \frac{D_{\infty}^{2}}{2\alpha_{1}(1-\beta_{1})} \sum_{i=1}^{d} (\sqrt{T\hat{v}_{T,i}} - \sqrt{\hat{v}_{1,i}} ) + \frac{D_{\infty}^{2}G_{\infty}}{2\alpha_{1}} \sum_{i=1}^{d} [\frac{\beta_{1,t}\sqrt{(t-1)} }{(1- \beta_{1,t})}] + \frac{\alpha_{1}(1+\beta_{1})}{(1-\beta_{1})}\frac{G_{\infty}}{(1-\gamma)\sqrt{1-\beta_{2}} } \sum_{i = 1}^{d}\left \| g_{1:T,i} \right \|_{2}\tag{带入公式(8)}\\ \end{eqnarray}\]

其中, \(\begin{eqnarray} \sum_{i=1}^{d} [\frac{\beta_{1,t}\sqrt{(t-1)} }{(1- \beta_{1,t})}] &\le& \sum_{i=1}^{d} \frac{1}{1-\beta_{1}}\lambda ^{t-1}\sqrt[]{t-1} \\ &\le& \sum_{i=1}^{d} \frac{1}{1-\beta_{1}}\lambda ^{t-1}(t-1) \\ &\le& \frac{1}{1-\beta_{1}} \frac {\lambda}{(1-\lambda)^2} \tag{16} \end{eqnarray}\)

注释:

\[\begin{eqnarray} \sum\limits_{n\ge0}nx^n &=& \sum\limits_{n\ge0}x(x^n)' \tag{求原函数,思路nx^{n-1}}\\ &=& x\sum\limits_{n\ge0}(x^n)' \\ &=& x\left(\sum\limits_{n\ge0}(x^n)\right)' \tag{常用的泰勒展开式} \\ &=& x\left(\frac1{1-x}\right)' \tag{|x|<1}\\ &=& \frac x{(1-x)^2} \end{eqnarray}\]

最后,

\[\begin{eqnarray} R(T) &\le& \sum_{i=1}^{d} [\frac{\sqrt{\hat{v}_{1,i}}D^{2}}{2\alpha_{1}(1- \beta_{1,1})} - \frac{\sqrt{\hat{v}_{T,i}}D^{2}}{2\alpha_{T}(1- \beta_{1,T})}] + \frac{D_{\infty}^{2}}{2\alpha_{1}(1-\beta_{1})} \sum_{i=1}^{d} (\sqrt{T\hat{v}_{T,i}} - \sqrt{\hat{v}_{1,i}} ) + \frac{D_{\infty}^{2}G_{\infty}}{2\alpha_{1}} \sum_{i=1}^{d} [\frac{\beta_{1,t}\sqrt{(t-1)} }{(1- \beta_{1,t})}] + \frac{\alpha_{1}(1+\beta_{1})}{(1-\beta_{1})}\frac{G_{\infty}}{(1-\gamma)\sqrt{1-\beta_{2}} } \sum_{i = 1}^{d}\left \| g_{1:T,i} \right \|_{2}\\ &\le& \sum_{i=1}^{d} [\frac{\sqrt{\hat{v}_{1,i}}D^{2}}{2\alpha_{1}(1- \beta_{1,1})} - \frac{\sqrt{T\hat{v}_{T,i}}D^{2}}{2\alpha_{1}(1- \beta_{1,T})}] + \frac{D_{\infty}^{2}}{2\alpha_{1}(1-\beta_{1})} \sum_{i=1}^{d} (\sqrt{T\hat{v}_{T,i}} - \sqrt{\hat{v}_{1,i}} ) + \sum_{i=1}^{d} \frac{\lambda D_{\infty}^{2} G_{\infty}}{2\alpha_{1}(1-\beta_{1})(1-\lambda)^2} + \frac{\alpha_{1}(1+\beta_{1}) G_{\infty}}{(1-\gamma)\sqrt{1-\beta_{2}}(1-\beta_{1}) } \sum_{i = 1}^{d}\left \| g_{1:T,i} \right \|_{2} \tag{带入公式(16)}\\ \end{eqnarray}\]

改进方向

ADAMAX

AdamW

AdamX

Code精读

Code

m, v = exp_avg, exp_avg_sq

\(m_{t} \gets \beta_{1} \cdot m_{t-1} + (1-\beta_{1})\cdot g_{t}\)
\(v_{t} \gets \beta_{2} \cdot v_{t-1} + (1-\beta_{2})\cdot g_{t}^{2}\)

m.mul_(beta1).add_(grad, alpha=1 - beta1)
v.mul_(beta2).addcmul_(grad, grad.conj(), value=1 - beta2)

偏差修正

bias_correction1 = 1 - beta1 ** step
bias_correction2 = 1 - beta2 ** step

更新参数向量\(\theta_{t}\)

\[\begin{align*} &\theta_{t} \gets \theta_{t-1} - \alpha \cdot \hat m_{t} / (\sqrt{\hat v_{t}} + \epsilon) \\ &\theta_{t} \gets \theta_{t-1} - \alpha \cdot \frac{m_{t}}{(1-\beta_{1}^{t})} / (\sqrt{\frac{v_{t}}{(1-\beta_{2}^{t})} } + \epsilon) \end{align*}\]

param.addcdiv_(m, denom, value=-step_size)

其中分母\(\sqrt{\frac{v_{t}}{(1-\beta_{2}^{t})} } + \epsilon\)

denom = (v.sqrt() / math.sqrt(bias_correction2)).add_(eps)

学习率\(\alpha_{t} = \frac{\alpha}{(1-\beta_{1}^{t})}\)

step_size = lr / bias_correction1

Adam of pytorch

\(\begin{aligned} & \hline \\ &\textbf{input} : \gamma \text{(lr)}, \: \beta_1, \beta_2 \text{(betas)}, \: \theta_0 \text{(params)}, \: f(\theta) \text{(objective)}, \: \epsilon \text{ (epsilon)} \\ &\hspace{13mm} \lambda \text{(weight decay)}, \: \textit{amsgrad}, \: \textit{maximize} \\ &\textbf{initialize} : m_0 \leftarrow 0 \text{ (first moment)}, v_0 \leftarrow 0 \text{ ( second moment)}, \: \widehat{v_0}^{max}\leftarrow 0 \\[-1.ex] & \hline \\ &\textbf{for} \: t=1 \: \textbf{to} \: \ldots \: \textbf{do} \\ &\hspace{5mm}\textbf{if} \: \textit{maximize}: \\ &\hspace{10mm}g_t \leftarrow -\nabla_{\theta} f_t (\theta_{t-1}) \\ &\hspace{5mm}\textbf{else} \\ &\hspace{10mm}g_t \leftarrow \nabla_{\theta} f_t (\theta_{t-1}) \\ &\hspace{5mm} \theta_t \leftarrow \theta_{t-1} - \gamma \lambda \theta_{t-1} \\ &\hspace{5mm}m_t \leftarrow \beta_1 m_{t-1} + (1 - \beta_1) g_t \\ &\hspace{5mm}v_t \leftarrow \beta_2 v_{t-1} + (1-\beta_2) g^2_t \\ &\hspace{5mm}\widehat{m_t} \leftarrow m_t/\big(1-\beta_1^t \big) \\ &\hspace{5mm}\widehat{v_t} \leftarrow v_t/\big(1-\beta_2^t \big) \\ &\hspace{5mm}\textbf{if} \: amsgrad \\ &\hspace{10mm}\widehat{v_t}^{max} \leftarrow \mathrm{max}(\widehat{v_t}^{max}, \widehat{v_t}) \\ &\hspace{10mm}\theta_t \leftarrow \theta_t - \gamma \widehat{m_t}/ \big(\sqrt{\widehat{v_t}^{max}} + \epsilon \big) \\ &\hspace{5mm}\textbf{else} \\ &\hspace{10mm}\theta_t \leftarrow \theta_t - \gamma \widehat{m_t}/ \big(\sqrt{\widehat{v_t}} + \epsilon \big) \\ & \hline \\[-1.ex] &\bf{return} \: \theta_t \\[-1.ex] & \hline \\[-1.ex] \end{aligned}\)

扩展

1. 随机梯度下降算法发展史: SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> RMSprop -> Adam -> AdaMax -> Nadam
2. An overview of gradient descent optimization algorithms∗
3. ON THE CONVERGENCE PROOF OF AMSGRAD AND A NEW VERSION?