Complete IoU Loss

Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

解决了什么问题

为了解决以下l损失函数的问题:

\[\left\{\begin{matrix} \begin{align} IoU &: 无法解决目标框与预测框无交集的情况\\ GIoU &: 收敛速度慢\\ DIoU &: 预测框与目标框不一致 \end{align} \end{matrix}\right.\]

在物体检测中, 通常用到的损失函数是IoU(Intersection over Union)和GIoU(generalized IoU), 虽然GIoU补充了IoU在两个box不重叠时候梯度消失无法检测的情况, 但是GIoU还是存在问题(收敛速度慢)

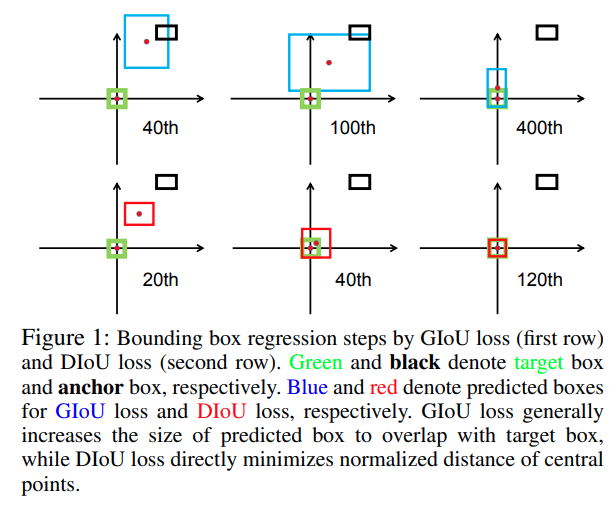
绿色框为真实目标框, 黑色框为首次出现的预测框, 蓝色框是GIoU_Loss预测框, 红色框为DIoU_Loss预测框.

当GIoU与目标框没有交集时, 它必须扩大自己的面积与目标产生交集, 这是导致它收敛慢的主要原因.所以DIoU的提出便是为了解决这个问题. 而DIoU依然存在一个问题, 预测框的大小和目标框不一致. CIoU_Loss的提出便是为了解决这一个问题

方法

\[\begin{eqnarray} \mathcal{L}_{CIoU} & = & 1 - IoU + \frac{\rho^{2}(\textbf{b},\textbf{b}^{gt})}{c^{2}} + \alpha \upsilon\\ v & = & \frac{4}{\pi^{2}} (arctan\frac{w^{gt}}{h^{gt}} - arctan\frac{w}{h})^{2}\\ \alpha & = & \frac{v}{(1-IoU) + v} \\ IoU & = & \frac{\left | B \cap B^{gt} \right | }{\left | B \cup B^{gt} \right |} \\ B^{gt} & = & (x^{gt}, y^{gt}, w^{gt}, h^{gt}) \\ B & = & (x, y, w, h) \end{eqnarray}\]

参数:

A	B	C
1	\(\textbf{b}^{gt}\)	真实目标框
2	\(\textbf{b}\)	预测框(x,y,w,h)或(x1,y1,x2,y2)
3	\(\rho\)	欧氏距离
4	\(c\)	真实框与预测框的最小包围框的对角线长度
5	\(\rho(\textbf{b},\textbf{b}^{gt})\)	真实框与预测框两中心的距离

检测算法

1. YOLOv3
2. SSD
3. Faster R-CNN

数据集

1. PASCAL VOC(VOC 2007和VOC 2012)
2. MS COCO 2017

效果

Distinguish

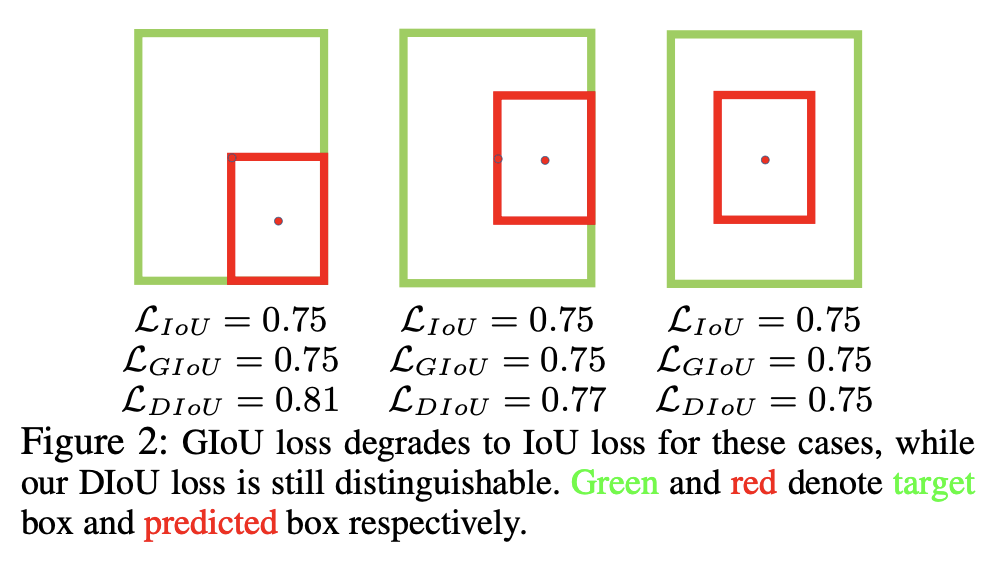
在GIoU和IoU这种情况下相同无法区分时, DIoU依然可以区分

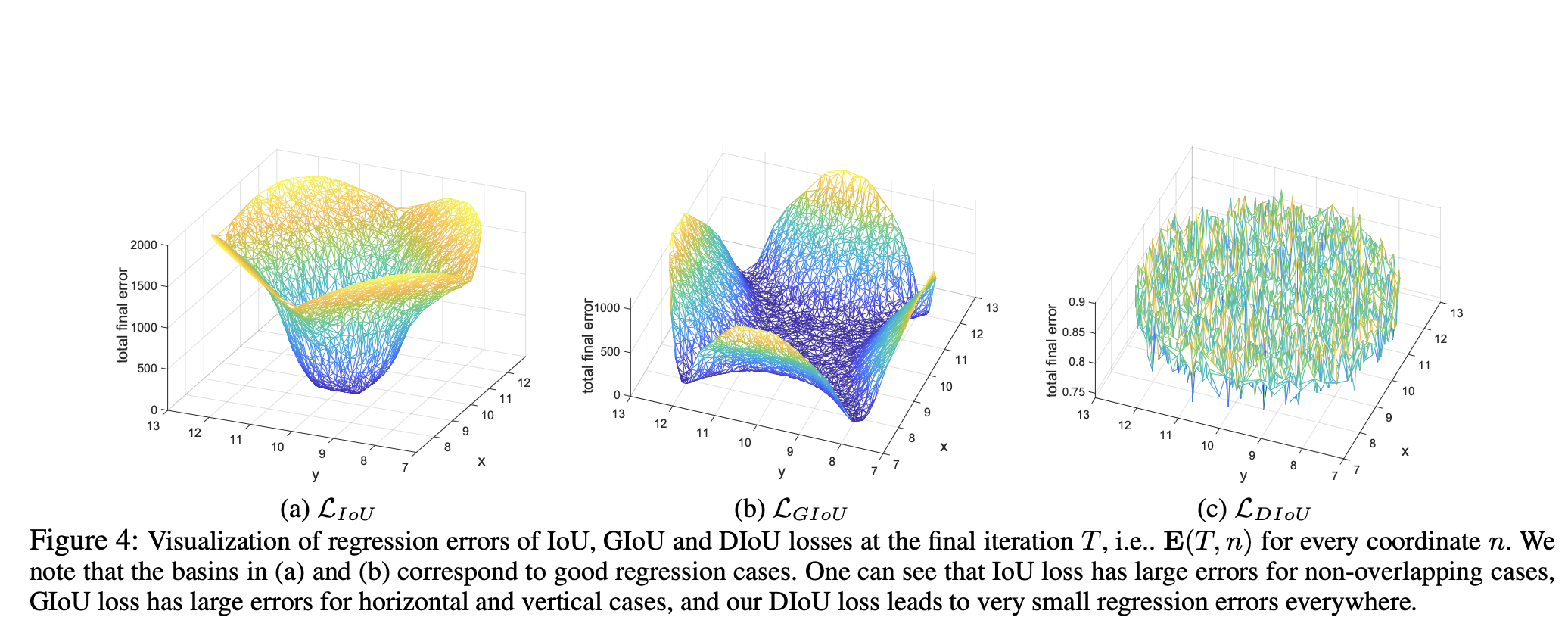
Regression error

在Fig4可以看到, 回归误差E(T,n)在DIoU上是最好的, 所有点都能处在一个低的误差范围

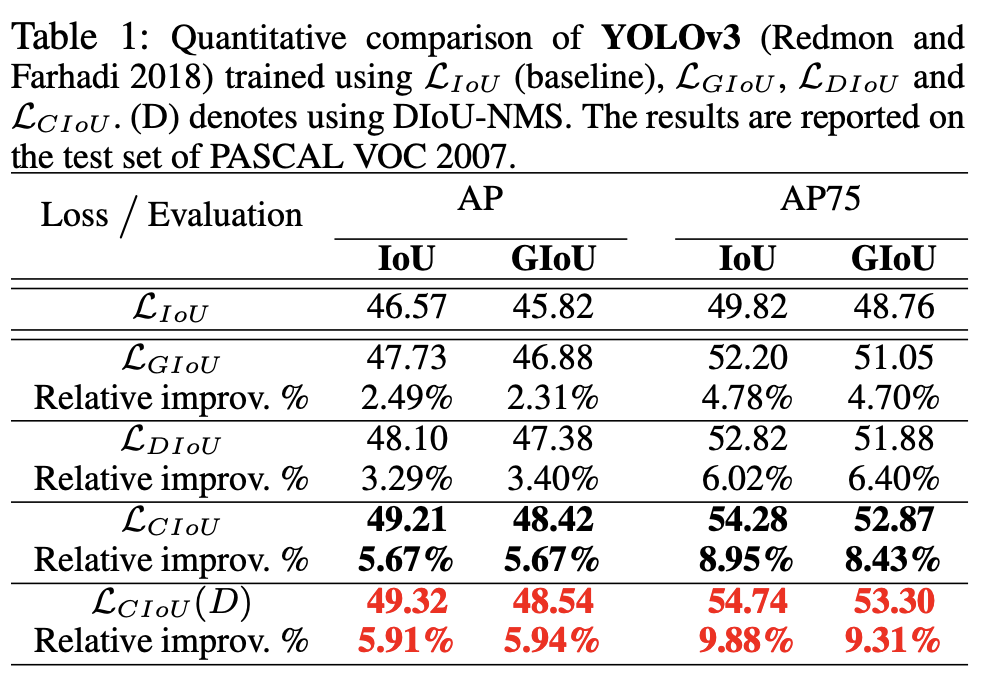
On YOLOv3 with PASCAL VOC 2007

DIoU loss 可以比IoU增加3.29% AP和6.02% AP75

On SSD with PASCAL VOC 2007

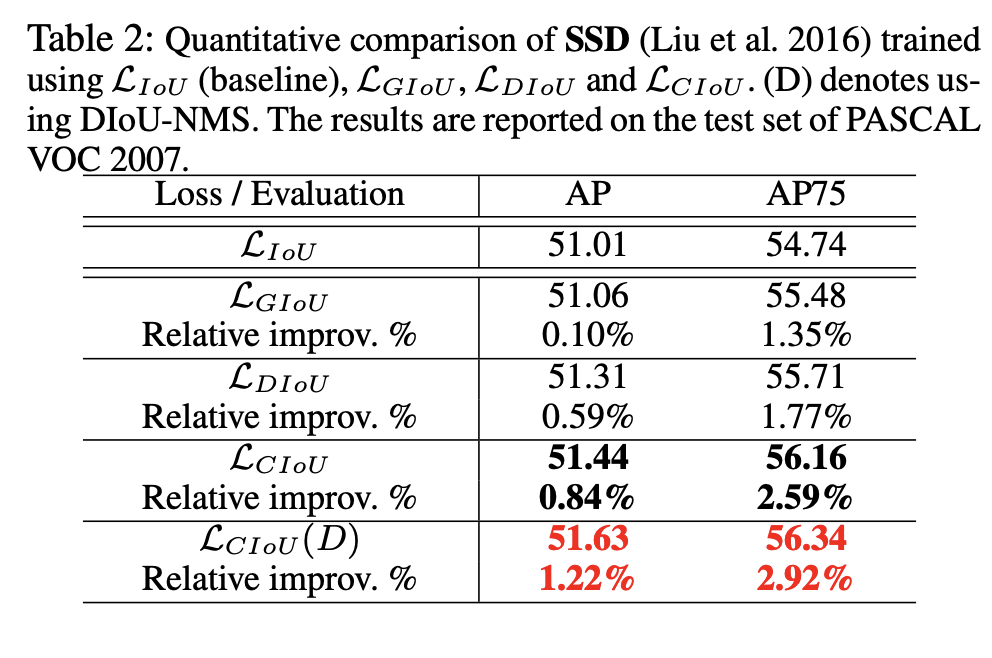
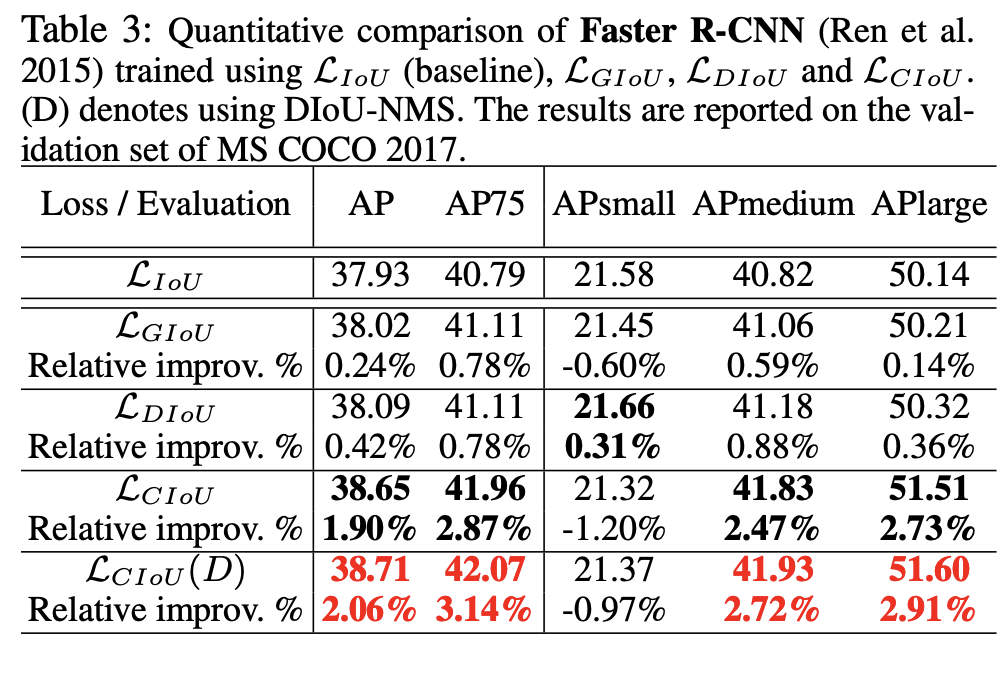
On Faster R-CNN with MS COCO 2017

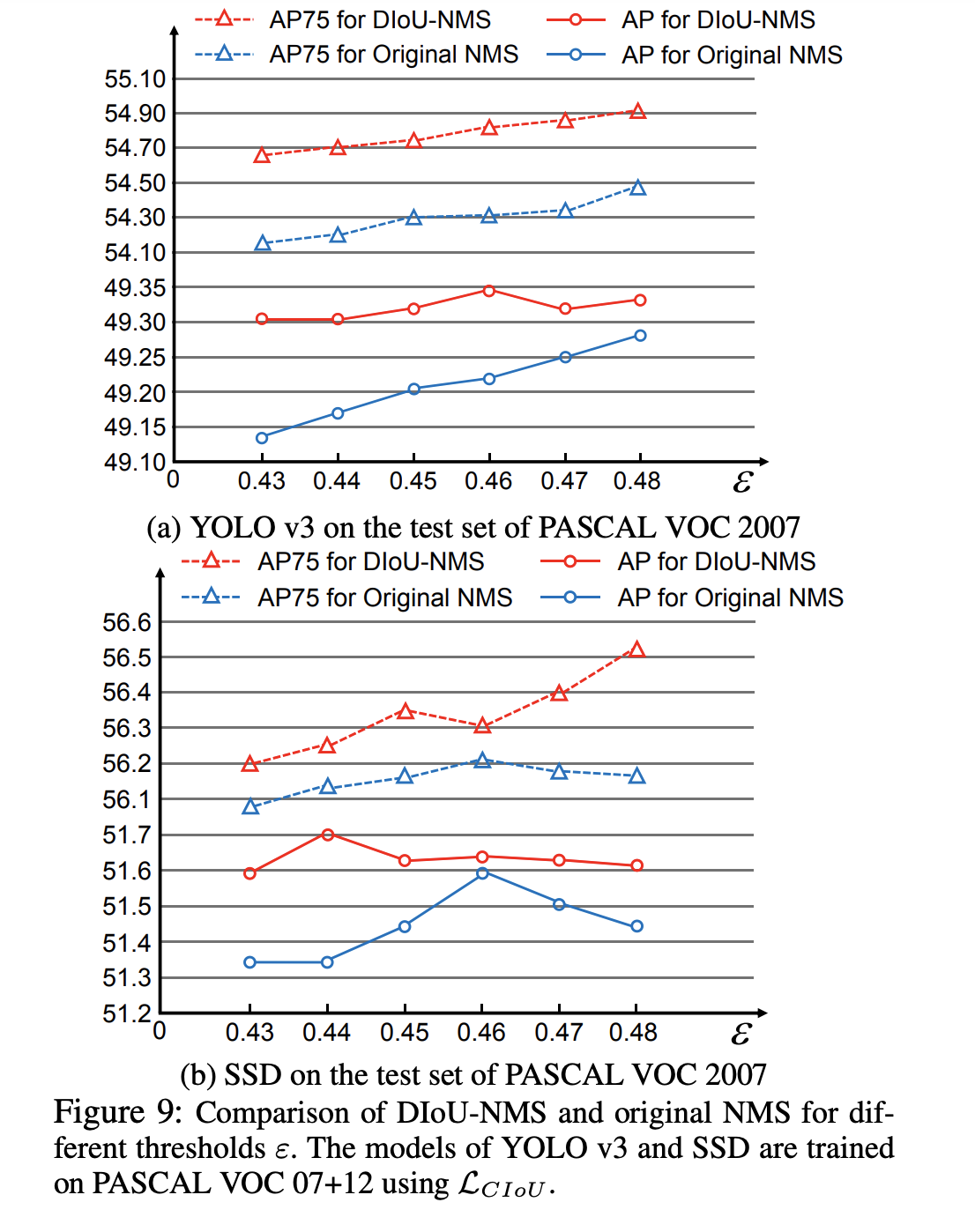
Comparison of DIoU_NMS and original NMS

我们在阈值为[0.43,0.48]范围内比较原NMS和DIoU_NMS。从图9可以看出，DIoU_NMS在各个方面都优于原NMS 所以不需要仔细调整阈值ε也能得到表现比原NMS好的结果。

改进方向

Alpha-IoU: A Family of Power Intersection over Union Losses for Bounding Box Regression

在所有IoU上添加一个α次方,由实验数据可知, \(\alpha \in [2,4]\)效果不错,且\(\alpha = 3\)时最好.

\[\begin{eqnarray}\mathcal{L}_{IoU} &=& 1 − IoU \Rightarrow \mathcal{L}_{\alpha-IoU} = 1 − IoU^{\alpha} \\ \mathcal{L}_{GIoU} &=& 1 − IoU +\frac{|C - B \cup B^{gt}|}{|C|} \Rightarrow \mathcal{L}_{\alpha -GIoU} = 1 − IoU^{\alpha} + (\frac{|C - B \cup B^{gt}|}{|C|})^{\alpha}\\ \mathcal{L}_{DIoU} &=& 1 − IoU +\frac{\rho^{2}(b, bgt)}{c^2} \Rightarrow \mathcal{L}_{\alpha-DIoU} = 1 − IoU^{\alpha} +\frac{\rho^{2\alpha }(b, b^{gt})}{c^{2\alpha} }\\ \mathcal{L}_{CIoU} &=& 1 − IoU +\frac{\rho^{2}(b, bgt)}{c^2}+ \beta v \Rightarrow \mathcal{L}_{\alpha -CIoU} = 1 − IoU^{\alpha} +\frac{\rho^{2\alpha}(b, b^{gt})}{c^{2\alpha}}+ (\beta v)^{\alpha }\end{eqnarray}\]

Code精读

def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, eps=1e-7):
    # Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
    box2 = box2.T #转置后形状(4,n)

    # Get the coordinates of bounding boxes
    if x1y1x2y2:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
        b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
    else:  # transform from xywh to xyxy
        b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
        b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
        b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
        b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2

    # 交集面积
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
            (torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)

    # 并集面积
    w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
    w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
    union = w1 * h1 + w2 * h2 - inter + eps

    iou = inter / union
    if GIoU or DIoU or CIoU:
        cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1)  # convex (smallest enclosing box) width最小包围框的宽
        ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1)  # convex height最小包围框的高
        if CIoU or DIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            c2 = cw ** 2 + ch ** 2 + eps  # convex diagonal squared最小包围框的对角线长度的平方
            rho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 +
                    (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4  # center distance squared两个框中心距离的平方
            if DIoU:
                return iou - rho2 / c2  # DIoU
            elif CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
                with torch.no_grad():
                    alpha = v / (v - iou + (1 + eps))
                return iou - (rho2 / c2 + v * alpha)  # CIoU
        else:  # GIoU https://arxiv.org/pdf/1902.09630.pdf
            c_area = cw * ch + eps  # convex area
            return iou - (c_area - union) / c_area  # GIoU
    else:
        return iou  # IoU

1. 此代码位于yolov5/utils/metrics.py, box1为预测框, box2为真实目标框.
2. 在yolov5/utils/loss.py中, 其x1y1x2y2=False,传入的box参数为(x,y,w,h)

   iou = bbox_iou(pbox.T, tbox[i], x1y1x2y2=False, CIoU=True)  # iou(prediction, target)
   lbox += (1.0 - iou).mean()  # iou loss
   

3. 在物体识别中, 坐标系原点一般为左上角, 整个图像处于第一象限,所以x,y没有负值, clamp(0)只会识别出两个框不相交的情况

扩展

在Yolov11中应用到的其它Loss

损失函数	使用场景	优点	缺点	论文出处
VarifocalLoss	目标检测中的分类任务，特别是处理不平衡数据（如前景和背景样本不平衡）。	1. 动态调整样本权重，关注难分类样本。 2. 适用于不平衡数据。	1. 计算复杂度较高。 2. 需要调整超参数（如 alpha 和 gamma）。	Varifocal Loss: A Dynamic Loss for Dense Object Detection
FocalLoss	目标检测中的分类任务，处理类别不平衡问题。	1. 减少易分类样本的损失贡献，关注难分类样本。 2. 缓解类别不平衡问题。	1. 需要调整超参数（如 gamma 和 alpha）。 2. 对噪声敏感。	Focal Loss for Dense Object Detection
DFLoss	目标检测中的边界框回归任务，用于预测边界框的分布。	1. 通过分布预测提高边界框回归精度。 2. 适用于密集目标检测。	1. 计算复杂度较高。 2. 需要调整 reg_max 参数。	Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
BboxLoss	目标检测中的边界框回归任务，结合 IoU 损失和 DFL 损失。	1. 结合 IoU 和 DFL，提高边界框回归精度。 2. 适用于通用目标检测任务。	1. 计算复杂度较高。 2. 需要调整超参数。	基于 IoU 和 DFL 的改进，无单独论文。
RotatedBboxLoss	旋转目标检测中的边界框回归任务，处理旋转边界框。	1. 支持旋转边界框的回归。 2. 适用于旋转目标检测任务。	1. 计算复杂度较高。 2. 需要调整超参数。	基于 IoU 和 DFL 的改进，无单独论文。
KeypointLoss	关键点检测任务，如人体姿态估计。	1. 支持关键点检测任务。 2. 通过欧氏距离计算损失。	1. 对关键点标注质量敏感。 2. 需要调整 sigmas 参数。	基于 COCO 关键点评估方法，无单独论文。
v8DetectionLoss	YOLOv8 目标检测任务，结合分类、边界框回归和 DFL 损失。	1. 综合性强，适用于通用目标检测。 2. 支持多任务学习。	1. 计算复杂度较高。 2. 需要调整超参数。	基于 YOLOv8 的改进，无单独论文。
v8SegmentationLoss	YOLOv8 实例分割任务，结合检测和分割损失。	1. 支持实例分割任务。 2. 结合检测和分割损失，提高分割精度。	1. 计算复杂度较高。 2. 需要调整超参数。	基于 YOLOv8 的改进，无单独论文。
v8PoseLoss	YOLOv8 姿态估计任务，结合关键点检测和分类损失。	1. 支持姿态估计任务。 2. 结合关键点检测和分类损失，提高姿态估计精度。	1. 计算复杂度较高。 2. 需要调整超参数。	基于 YOLOv8 的改进，无单独论文。
v8ClassificationLoss	YOLOv8 分类任务，用于图像分类。	1. 简单高效，适用于分类任务。 2. 使用交叉熵损失，易于实现。	1. 仅适用于分类任务，不支持多任务学习。	基于交叉熵损失的改进，无单独论文。
v8OBBLoss	YOLOv8 旋转目标检测任务，处理旋转边界框。	1. 支持旋转目标检测任务。 2. 结合分类、边界框回归和 DFL 损失。	1. 计算复杂度较高。 2. 需要调整超参数。	基于 YOLOv8 的改进，无单独论文。
E2EDetectLoss	端到端目标检测任务，结合一对多和一对一检测策略。	1. 结合一对多和一对一检测，提高检测精度。 2. 适用于端到端检测任务。	1. 计算复杂度较高。 2. 需要调整超参数。	基于 YOLOv8 的改进，无单独论文。

VarifocalLoss

\(L = \alpha \cdot p^\gamma \cdot (1 - q) + q \cdot \text{BCE}(p, q)\)

class VarifocalLoss(nn.Module):
    """
    Varifocal loss by Zhang et al.

    https://arxiv.org/abs/2008.13367.
    """

    def __init__(self):
        """Initialize the VarifocalLoss class."""
        super().__init__()

    @staticmethod
    def forward(pred_score, gt_score, label, alpha=0.75, gamma=2.0):
        """Computes varfocal loss."""
        weight = alpha * pred_score.sigmoid().pow(gamma) * (1 - label) + gt_score * label
        with autocast(enabled=False):
            loss = (
                (F.binary_cross_entropy_with_logits(pred_score.float(), gt_score.float(), reduction="none") * weight)
                .mean(1)
                .sum()
            )
        return loss

FocalLoss

\(L = -\alpha_t (1 - p_t)^\gamma \log(p_t)\)

class FocalLoss(nn.Module):
    """Wraps focal loss around existing loss_fcn(), i.e. criteria = FocalLoss(nn.BCEWithLogitsLoss(), gamma=1.5)."""

    def __init__(self):
        """Initializer for FocalLoss class with no parameters."""
        super().__init__()

    @staticmethod
    def forward(pred, label, gamma=1.5, alpha=0.25):
        """Calculates and updates confusion matrix for object detection/classification tasks."""
        loss = F.binary_cross_entropy_with_logits(pred, label, reduction="none")
        # p_t = torch.exp(-loss)
        # loss *= self.alpha * (1.000001 - p_t) ** self.gamma  # non-zero power for gradient stability

        # TF implementation https://github.com/tensorflow/addons/blob/v0.7.1/tensorflow_addons/losses/focal_loss.py
        pred_prob = pred.sigmoid()  # prob from logits
        p_t = label * pred_prob + (1 - label) * (1 - pred_prob)
        modulating_factor = (1.0 - p_t) ** gamma
        loss *= modulating_factor
        if alpha > 0:
            alpha_factor = label * alpha + (1 - label) * (1 - alpha)
            loss *= alpha_factor
        return loss.mean(1).sum()

DFLoss

\(L = \text{CrossEntropy}(p, y_l) \cdot w_l + \text{CrossEntropy}(p, y_r) \cdot w_r\)

class DFLoss(nn.Module):
    """Criterion class for computing DFL losses during training."""

    def __init__(self, reg_max=16) -> None:
        """Initialize the DFL module."""
        super().__init__()
        self.reg_max = reg_max

    def __call__(self, pred_dist, target):
        """
        Return sum of left and right DFL losses.

        Distribution Focal Loss (DFL) proposed in Generalized Focal Loss
        https://ieeexplore.ieee.org/document/9792391
        """
        target = target.clamp_(0, self.reg_max - 1 - 0.01)
        tl = target.long()  # target left
        tr = tl + 1  # target right
        wl = tr - target  # weight left
        wr = 1 - wl  # weight right
        return (
            F.cross_entropy(pred_dist, tl.view(-1), reduction="none").view(tl.shape) * wl
            + F.cross_entropy(pred_dist, tr.view(-1), reduction="none").view(tl.shape) * wr
        ).mean(-1, keepdim=True)

BboxLoss

\[\begin{align} \text{FG 表示所有正样本的集合} \\ w_i &= \sum_j \text{target_scores}_{ij} \\ S &= \text{target_scores_sum 是正样本目标得分的总和} \\ \text{IoU 损失：} L_{iou} &= \frac{1}{S} \sum_{i \in \text{FG}} w_i \cdot \left(1 - \text{IoU}(\hat{b}_i, b_i)\right) \quad \text{if reg_max} \le 1 \\ \text{DFL 损失：} L_{dfl} &= \frac{1}{S} \sum_{i \in \text{FG}} w_i \cdot \text{DFLoss}(\text{pred_dist}_i, t_i) \quad \text{if reg_max} > 1 \end{align}\]

class BboxLoss(nn.Module):
    """Criterion class for computing training losses during training."""

    def __init__(self, reg_max=16):
        """Initialize the BboxLoss module with regularization maximum and DFL settings."""
        super().__init__()
        self.dfl_loss = DFLoss(reg_max) if reg_max > 1 else None

    def forward(self, pred_dist, pred_bboxes, anchor_points, target_bboxes, target_scores, target_scores_sum, fg_mask):
        """IoU loss."""
        weight = target_scores.sum(-1)[fg_mask].unsqueeze(-1)
        iou = bbox_iou(pred_bboxes[fg_mask], target_bboxes[fg_mask], xywh=False, CIoU=True)
        loss_iou = ((1.0 - iou) * weight).sum() / target_scores_sum

        # DFL loss
        if self.dfl_loss:
            target_ltrb = bbox2dist(anchor_points, target_bboxes, self.dfl_loss.reg_max - 1)
            loss_dfl = self.dfl_loss(pred_dist[fg_mask].view(-1, self.dfl_loss.reg_max), target_ltrb[fg_mask]) * weight
            loss_dfl = loss_dfl.sum() / target_scores_sum
        else:
            loss_dfl = torch.tensor(0.0).to(pred_dist.device)

        return loss_iou, loss_dfl

RotatedBboxLoss

\[\begin{align} \mathcal{F} \text{ 表示所有正样本的集合} \\ w_i &= \sum_j \text{target_scores}_{ij} \\ S &= \sum_{i \in \mathcal{F}} w_i \text{ 是正样本目标得分的总和, 归一化因子} \\ L_{iou} &= \frac{1}{S} \sum_{i \in \mathcal{F}} w_i \cdot \left(1 - \text{probiou}(\hat{b}_i, b_i)\right) \quad \text{if reg_max} \le 1 \\ L_{dfl} &= \frac{1}{S} \sum_{i \in \mathcal{F}} w_i \cdot \text{DFLoss}(\text{pred_dist}_i, t_i) \quad \text{if reg_max} > 1 \end{align}\]

class RotatedBboxLoss(BboxLoss):
    """Criterion class for computing training losses during training."""

    def __init__(self, reg_max):
        """Initialize the BboxLoss module with regularization maximum and DFL settings."""
        super().__init__(reg_max)

    def forward(self, pred_dist, pred_bboxes, anchor_points, target_bboxes, target_scores, target_scores_sum, fg_mask):
        """IoU loss."""
        weight = target_scores.sum(-1)[fg_mask].unsqueeze(-1)
        iou = probiou(pred_bboxes[fg_mask], target_bboxes[fg_mask])
        loss_iou = ((1.0 - iou) * weight).sum() / target_scores_sum

        # DFL loss
        if self.dfl_loss:
            target_ltrb = bbox2dist(anchor_points, xywh2xyxy(target_bboxes[..., :4]), self.dfl_loss.reg_max - 1)
            loss_dfl = self.dfl_loss(pred_dist[fg_mask].view(-1, self.dfl_loss.reg_max), target_ltrb[fg_mask]) * weight
            loss_dfl = loss_dfl.sum() / target_scores_sum
        else:
            loss_dfl = torch.tensor(0.0).to(pred_dist.device)

        return loss_iou, loss_dfl

其中probiou是计算基于高斯分布的 IoU，它使用协方差矩阵和Bhattacharyya距离衡量 OBB 之间的不确定性差异。

1. 输入 OBB 数据：函数接收两个形状为 (N,5) 的张量，表示 N 个旋转边界框，格式为 (x, y, w, h, r)。
2. 计算中心坐标：拆分输入 OBB，获取 (x, y) 作为中心坐标。
3. 计算协方差矩阵：
   • _get_covariance_matrix(obb) 计算每个 OBB 的协方差矩阵的参数 (a, b, c)，表示高斯分布的形状。 \(\begin{aligned}a_i &= \frac{w_i^2}{12}\cos^2 r_i + \frac{h_i^2}{12}\sin^2 r_i, \\ b_i &= \frac{w_i^2}{12}\sin^2 r_i + \frac{h_i^2}{12}\cos^2 r_i, \\ c_i &= \left(\frac{w_i^2}{12} - \frac{h_i^2}{12}\right)\cos r_i\,\sin r_i, \end{aligned}\)
4. 计算 Bhattacharyya 距离（BD）：
   • T1 计算中心点分布差异；
   • T2 计算相关性项；
   • T3 计算协方差矩阵的相似性项；
   • BD = T1 + T2 + T3，限制 BD 取值范围以保持数值稳定性。 \(\begin{cases} t_1 = \frac{1}{4} \cdot \frac{(a_1+a_2)(y_1-y_2)^2 + (b_1+b_2)(x_1-x_2)^2}{(a_1+a_2)(b_1+b_2) - (c_1+c_2)^2 + \epsilon}\\ t_2 = \frac{1}{2} \cdot \frac{(c_1+c_2)(x_2-x_1)(y_1-y_2)}{(a_1+a_2)(b_1+b_2) - (c_1+c_2)^2 + \epsilon}\\ t_3 = \frac{1}{2} \cdot \ln\!\left(\frac{(a_1+a_2)(b_1+b_2) - (c_1+c_2)^2}{4 \sqrt{\max\{0,\,a_1b_1-c_1^2\}\cdot\max\{0,\,a_2b_2-c_2^2\}} + \epsilon} + \epsilon\right) \end{cases}\)
5. 计算 Hellinger 距离（HD）：
   • HD = sqrt(1 - exp(-BD))，用于转换 BD 到相似度衡量。
   • Hellinger 距离的离散概率分布计算公式：\(H(P,Q)=\sqrt[]{\frac{1}{2} \sum_{i}^{}(\sqrt[]{p_i}-\sqrt[]{q_i} })^2\)
6. 计算最终的 Probiou：
   • IoU = 1 - HD，得到 Probiou 评分。
7. 可选 CIoU 计算：
   • 计算宽高比的影响 v；
   • 计算 alpha 作为权重调整 IoU；
   • return iou - v * alpha 返回 CIoU 结果。

def probiou(obb1, obb2, CIoU=False, eps=1e-7):
    """
    计算两个旋转边界框（OBB）的概率 IoU（Probiou）。
    
    该方法基于论文 https://arxiv.org/pdf/2106.06072v1.pdf 实现。
    它采用 Bhattacharyya 距离（BD）和 Hellinger 距离（HD）计算两个 OBB 的相似度。

    Args:
        obb1 (torch.Tensor): 真实 OBBs, 形状 (N, 5)，格式为 (x, y, w, h, r)。
        obb2 (torch.Tensor): 预测 OBBs, 形状 (N, 5)，格式为 (x, y, w, h, r)。
        CIoU (bool, optional): 是否计算 CIoU，默认为 False。
        eps (float, optional): 避免除零错误的小数值，默认为 1e-7。

    Returns:
        torch.Tensor: 计算得到的 OBB 相似度分数，形状 (N, )。

    备注:
        OBB 格式: [中心 x, 中心 y, 宽度 w, 高度 h, 旋转角度 r]。
        若 CIoU=True，则返回 CIoU 而不是普通的 Probiou。
    """
    # 提取中心坐标
    x1, y1 = obb1[..., :2].split(1, dim=-1)  # 真实框中心
    x2, y2 = obb2[..., :2].split(1, dim=-1)  # 预测框中心

    # 计算两个 OBB 的协方差矩阵
    a1, b1, c1 = _get_covariance_matrix(obb1)  # OBB1 的协方差矩阵参数
    a2, b2, c2 = _get_covariance_matrix(obb2)  # OBB2 的协方差矩阵参数

    # 计算 Bhattacharyya 距离的三部分
    # T1: 计算两个边界框的中心点分布差异
    t1 = (
        ((a1 + a2) * (y1 - y2).pow(2) + (b1 + b2) * (x1 - x2).pow(2)) /
        ((a1 + a2) * (b1 + b2) - (c1 + c2).pow(2) + eps)
    ) * 0.25

    # T2: 计算相关性项
    t2 = (
        ((c1 + c2) * (x2 - x1) * (y1 - y2)) /
        ((a1 + a2) * (b1 + b2) - (c1 + c2).pow(2) + eps)
    ) * 0.5

    # T3: 计算协方差矩阵之间的相似度
    t3 = (
        ((a1 + a2) * (b1 + b2) - (c1 + c2).pow(2)) /
        (4 * ((a1 * b1 - c1.pow(2)).clamp_(0) * (a2 * b2 - c2.pow(2)).clamp_(0)).sqrt() + eps)
        + eps
    ).log() * 0.5

    # 计算 Bhattacharyya 距离（BD）
    bd = (t1 + t2 + t3).clamp(eps, 100.0)  # 限制 BD 取值范围，避免过大影响计算

    # 计算 Hellinger 距离（HD）
    hd = (1.0 - (-bd).exp() + eps).sqrt()  # HD 通过 BD 指数化处理

    # 计算最终的 Probiou 值
    iou = 1 - hd  # Probiou 计算公式

    # 若启用 CIoU，则加入长宽比因素
    if CIoU:
        # 提取宽高
        w1, h1 = obb1[..., 2:4].split(1, dim=-1)
        w2, h2 = obb2[..., 2:4].split(1, dim=-1)

        # 计算宽高比的影响
        v = (4 / math.pi**2) * ((w2 / h2).atan() - (w1 / h1).atan()).pow(2)

        # 计算 alpha 权重
        with torch.no_grad():
            alpha = v / (v - iou + (1 + eps))

        # 计算最终 CIoU 值
        return iou - v * alpha

    return iou

KeypointLoss

\[\begin{cases} d_{i,k} &= \left(x_{i,k}^{\text{pred}} - x_{i,k}^{\text{gt}}\right)^2 + \left(y_{i,k}^{\text{pred}} - y_{i,k}^{\text{gt}}\right)^2, \text{对于每个样本 i 中的每个关键点 k} \\ e_{i,k} &= \frac{d_{i,k}}{8\,\sigma_k^2 \cdot (A_i + \epsilon)}, \quad A_i = \text{目标区域面积}, \sigma_k = \text{标准差} \\ l_{i,k} &= 1 - e^\left(-e_{i,k}\right) \\ \lambda_i &= \frac{K}{\sum_{k=1}^{K} m_{i,k} + \epsilon}, \quad K = \text{关键点总数(即 kpt_mask.shape[1])}, m_{i,k} = \text{关键点掩码，若该关键点有效则为 1，否则为 0} \\ L &= \frac{1}{N \times K} \sum_{i=1}^{N} \lambda_i \sum_{k=1}^{K} m_{i,k} \cdot l_{i,k}, \quad \text{N 是批次中的样本数} \end{cases}\]

class KeypointLoss(nn.Module):
    """Criterion class for computing training losses."""

    def __init__(self, sigmas) -> None:
        """Initialize the KeypointLoss class."""
        super().__init__()
        self.sigmas = sigmas

    def forward(self, pred_kpts, gt_kpts, kpt_mask, area):
        """Calculates keypoint loss factor and Euclidean distance loss for predicted and actual keypoints."""
        d = (pred_kpts[..., 0] - gt_kpts[..., 0]).pow(2) + (pred_kpts[..., 1] - gt_kpts[..., 1]).pow(2)
        kpt_loss_factor = kpt_mask.shape[1] / (torch.sum(kpt_mask != 0, dim=1) + 1e-9)
        # e = d / (2 * (area * self.sigmas) ** 2 + 1e-9)  # from formula
        e = d / ((2 * self.sigmas).pow(2) * (area + 1e-9) * 2)  # from cocoeval
        return (kpt_loss_factor.view(-1, 1) * ((1 - torch.exp(-e)) * kpt_mask)).mean()

v8DetectionLoss

\[L = L_{cls} + L_{box} + L_{dfl}\]

class v8DetectionLoss:
    """Criterion class for computing training losses."""

    def __init__(self, model, tal_topk=10):  # model must be de-paralleled
        """Initializes v8DetectionLoss with the model, defining model-related properties and BCE loss function."""
        device = next(model.parameters()).device  # get model device
        h = model.args  # hyperparameters

        m = model.model[-1]  # Detect() module
        self.bce = nn.BCEWithLogitsLoss(reduction="none")
        self.hyp = h
        self.stride = m.stride  # model strides
        self.nc = m.nc  # number of classes
        self.no = m.nc + m.reg_max * 4
        self.reg_max = m.reg_max
        self.device = device

        self.use_dfl = m.reg_max > 1

        self.assigner = TaskAlignedAssigner(topk=tal_topk, num_classes=self.nc, alpha=0.5, beta=6.0)
        self.bbox_loss = BboxLoss(m.reg_max).to(device)
        self.proj = torch.arange(m.reg_max, dtype=torch.float, device=device)

    def preprocess(self, targets, batch_size, scale_tensor):
        """Preprocesses the target counts and matches with the input batch size to output a tensor."""
        nl, ne = targets.shape
        if nl == 0:
            out = torch.zeros(batch_size, 0, ne - 1, device=self.device)
        else:
            i = targets[:, 0]  # image index
            _, counts = i.unique(return_counts=True)
            counts = counts.to(dtype=torch.int32)
            out = torch.zeros(batch_size, counts.max(), ne - 1, device=self.device)
            for j in range(batch_size):
                matches = i == j
                if n := matches.sum():
                    out[j, :n] = targets[matches, 1:]
            out[..., 1:5] = xywh2xyxy(out[..., 1:5].mul_(scale_tensor))
        return out

    def bbox_decode(self, anchor_points, pred_dist):
        """Decode predicted object bounding box coordinates from anchor points and distribution."""
        if self.use_dfl:
            b, a, c = pred_dist.shape  # batch, anchors, channels
            pred_dist = pred_dist.view(b, a, 4, c // 4).softmax(3).matmul(self.proj.type(pred_dist.dtype))
            # pred_dist = pred_dist.view(b, a, c // 4, 4).transpose(2,3).softmax(3).matmul(self.proj.type(pred_dist.dtype))
            # pred_dist = (pred_dist.view(b, a, c // 4, 4).softmax(2) * self.proj.type(pred_dist.dtype).view(1, 1, -1, 1)).sum(2)
        return dist2bbox(pred_dist, anchor_points, xywh=False)

    def __call__(self, preds, batch):
        """Calculate the sum of the loss for box, cls and dfl multiplied by batch size."""
        loss = torch.zeros(3, device=self.device)  # box, cls, dfl
        feats = preds[1] if isinstance(preds, tuple) else preds
        pred_distri, pred_scores = torch.cat([xi.view(feats[0].shape[0], self.no, -1) for xi in feats], 2).split(
            (self.reg_max * 4, self.nc), 1
        )

        pred_scores = pred_scores.permute(0, 2, 1).contiguous()
        pred_distri = pred_distri.permute(0, 2, 1).contiguous()

        dtype = pred_scores.dtype
        batch_size = pred_scores.shape[0]
        imgsz = torch.tensor(feats[0].shape[2:], device=self.device, dtype=dtype) * self.stride[0]  # image size (h,w)
        anchor_points, stride_tensor = make_anchors(feats, self.stride, 0.5)

        # Targets
        targets = torch.cat((batch["batch_idx"].view(-1, 1), batch["cls"].view(-1, 1), batch["bboxes"]), 1)
        targets = self.preprocess(targets.to(self.device), batch_size, scale_tensor=imgsz[[1, 0, 1, 0]])
        gt_labels, gt_bboxes = targets.split((1, 4), 2)  # cls, xyxy
        mask_gt = gt_bboxes.sum(2, keepdim=True).gt_(0.0)

        # Pboxes
        pred_bboxes = self.bbox_decode(anchor_points, pred_distri)  # xyxy, (b, h*w, 4)
        # dfl_conf = pred_distri.view(batch_size, -1, 4, self.reg_max).detach().softmax(-1)
        # dfl_conf = (dfl_conf.amax(-1).mean(-1) + dfl_conf.amax(-1).amin(-1)) / 2

        _, target_bboxes, target_scores, fg_mask, _ = self.assigner(
            # pred_scores.detach().sigmoid() * 0.8 + dfl_conf.unsqueeze(-1) * 0.2,
            pred_scores.detach().sigmoid(),
            (pred_bboxes.detach() * stride_tensor).type(gt_bboxes.dtype),
            anchor_points * stride_tensor,
            gt_labels,
            gt_bboxes,
            mask_gt,
        )

        target_scores_sum = max(target_scores.sum(), 1)

        # Cls loss
        # loss[1] = self.varifocal_loss(pred_scores, target_scores, target_labels) / target_scores_sum  # VFL way
        loss[1] = self.bce(pred_scores, target_scores.to(dtype)).sum() / target_scores_sum  # BCE

        # Bbox loss
        if fg_mask.sum():
            target_bboxes /= stride_tensor
            loss[0], loss[2] = self.bbox_loss(
                pred_distri, pred_bboxes, anchor_points, target_bboxes, target_scores, target_scores_sum, fg_mask
            )

        loss[0] *= self.hyp.box  # box gain
        loss[1] *= self.hyp.cls  # cls gain
        loss[2] *= self.hyp.dfl  # dfl gain

        return loss.sum() * batch_size, loss.detach()  # loss(box, cls, dfl)

v8SegmentationLoss

\[L = L_{box} + L_{cls} + L_{dfl} + L_{mask}\]

class v8SegmentationLoss(v8DetectionLoss):
    """Criterion class for computing training losses."""

    def __init__(self, model):  # model must be de-paralleled
        """Initializes the v8SegmentationLoss class, taking a de-paralleled model as argument."""
        super().__init__(model)
        self.overlap = model.args.overlap_mask

    def __call__(self, preds, batch):
        """Calculate and return the loss for the YOLO model."""
        loss = torch.zeros(4, device=self.device)  # box, cls, dfl
        feats, pred_masks, proto = preds if len(preds) == 3 else preds[1]
        batch_size, _, mask_h, mask_w = proto.shape  # batch size, number of masks, mask height, mask width
        pred_distri, pred_scores = torch.cat([xi.view(feats[0].shape[0], self.no, -1) for xi in feats], 2).split(
            (self.reg_max * 4, self.nc), 1
        )

        # B, grids, ..
        pred_scores = pred_scores.permute(0, 2, 1).contiguous()
        pred_distri = pred_distri.permute(0, 2, 1).contiguous()
        pred_masks = pred_masks.permute(0, 2, 1).contiguous()

        dtype = pred_scores.dtype
        imgsz = torch.tensor(feats[0].shape[2:], device=self.device, dtype=dtype) * self.stride[0]  # image size (h,w)
        anchor_points, stride_tensor = make_anchors(feats, self.stride, 0.5)

        # Targets
        try:
            batch_idx = batch["batch_idx"].view(-1, 1)
            targets = torch.cat((batch_idx, batch["cls"].view(-1, 1), batch["bboxes"]), 1)
            targets = self.preprocess(targets.to(self.device), batch_size, scale_tensor=imgsz[[1, 0, 1, 0]])
            gt_labels, gt_bboxes = targets.split((1, 4), 2)  # cls, xyxy
            mask_gt = gt_bboxes.sum(2, keepdim=True).gt_(0.0)
        except RuntimeError as e:
            raise TypeError(
                "ERROR ❌ segment dataset incorrectly formatted or not a segment dataset.\n"
                "This error can occur when incorrectly training a 'segment' model on a 'detect' dataset, "
                "i.e. 'yolo train model=yolo11n-seg.pt data=coco8.yaml'.\nVerify your dataset is a "
                "correctly formatted 'segment' dataset using 'data=coco8-seg.yaml' "
                "as an example.\nSee https://docs.ultralytics.com/datasets/segment/ for help."
            ) from e

        # Pboxes
        pred_bboxes = self.bbox_decode(anchor_points, pred_distri)  # xyxy, (b, h*w, 4)

        _, target_bboxes, target_scores, fg_mask, target_gt_idx = self.assigner(
            pred_scores.detach().sigmoid(),
            (pred_bboxes.detach() * stride_tensor).type(gt_bboxes.dtype),
            anchor_points * stride_tensor,
            gt_labels,
            gt_bboxes,
            mask_gt,
        )

        target_scores_sum = max(target_scores.sum(), 1)

        # Cls loss
        # loss[1] = self.varifocal_loss(pred_scores, target_scores, target_labels) / target_scores_sum  # VFL way
        loss[2] = self.bce(pred_scores, target_scores.to(dtype)).sum() / target_scores_sum  # BCE

        if fg_mask.sum():
            # Bbox loss
            loss[0], loss[3] = self.bbox_loss(
                pred_distri,
                pred_bboxes,
                anchor_points,
                target_bboxes / stride_tensor,
                target_scores,
                target_scores_sum,
                fg_mask,
            )
            # Masks loss
            masks = batch["masks"].to(self.device).float()
            if tuple(masks.shape[-2:]) != (mask_h, mask_w):  # downsample
                masks = F.interpolate(masks[None], (mask_h, mask_w), mode="nearest")[0]

            loss[1] = self.calculate_segmentation_loss(
                fg_mask, masks, target_gt_idx, target_bboxes, batch_idx, proto, pred_masks, imgsz, self.overlap
            )

        # WARNING: lines below prevent Multi-GPU DDP 'unused gradient' PyTorch errors, do not remove
        else:
            loss[1] += (proto * 0).sum() + (pred_masks * 0).sum()  # inf sums may lead to nan loss

        loss[0] *= self.hyp.box  # box gain
        loss[1] *= self.hyp.box  # seg gain
        loss[2] *= self.hyp.cls  # cls gain
        loss[3] *= self.hyp.dfl  # dfl gain

        return loss.sum() * batch_size, loss.detach()  # loss(box, cls, dfl)

    @staticmethod
    def single_mask_loss(
        gt_mask: torch.Tensor, pred: torch.Tensor, proto: torch.Tensor, xyxy: torch.Tensor, area: torch.Tensor
    ) -> torch.Tensor:
        """
        Compute the instance segmentation loss for a single image.

        Args:
            gt_mask (torch.Tensor): Ground truth mask of shape (n, H, W), where n is the number of objects.
            pred (torch.Tensor): Predicted mask coefficients of shape (n, 32).
            proto (torch.Tensor): Prototype masks of shape (32, H, W).
            xyxy (torch.Tensor): Ground truth bounding boxes in xyxy format, normalized to [0, 1], of shape (n, 4).
            area (torch.Tensor): Area of each ground truth bounding box of shape (n,).

        Returns:
            (torch.Tensor): The calculated mask loss for a single image.

        Notes:
            The function uses the equation pred_mask = torch.einsum('in,nhw->ihw', pred, proto) to produce the
            predicted masks from the prototype masks and predicted mask coefficients.
        """
        pred_mask = torch.einsum("in,nhw->ihw", pred, proto)  # (n, 32) @ (32, 80, 80) -> (n, 80, 80)
        loss = F.binary_cross_entropy_with_logits(pred_mask, gt_mask, reduction="none")
        return (crop_mask(loss, xyxy).mean(dim=(1, 2)) / area).sum()

    def calculate_segmentation_loss(
        self,
        fg_mask: torch.Tensor,
        masks: torch.Tensor,
        target_gt_idx: torch.Tensor,
        target_bboxes: torch.Tensor,
        batch_idx: torch.Tensor,
        proto: torch.Tensor,
        pred_masks: torch.Tensor,
        imgsz: torch.Tensor,
        overlap: bool,
    ) -> torch.Tensor:
        """
        Calculate the loss for instance segmentation.

        Args:
            fg_mask (torch.Tensor): A binary tensor of shape (BS, N_anchors) indicating which anchors are positive.
            masks (torch.Tensor): Ground truth masks of shape (BS, H, W) if `overlap` is False, otherwise (BS, ?, H, W).
            target_gt_idx (torch.Tensor): Indexes of ground truth objects for each anchor of shape (BS, N_anchors).
            target_bboxes (torch.Tensor): Ground truth bounding boxes for each anchor of shape (BS, N_anchors, 4).
            batch_idx (torch.Tensor): Batch indices of shape (N_labels_in_batch, 1).
            proto (torch.Tensor): Prototype masks of shape (BS, 32, H, W).
            pred_masks (torch.Tensor): Predicted masks for each anchor of shape (BS, N_anchors, 32).
            imgsz (torch.Tensor): Size of the input image as a tensor of shape (2), i.e., (H, W).
            overlap (bool): Whether the masks in `masks` tensor overlap.

        Returns:
            (torch.Tensor): The calculated loss for instance segmentation.

        Notes:
            The batch loss can be computed for improved speed at higher memory usage.
            For example, pred_mask can be computed as follows:
                pred_mask = torch.einsum('in,nhw->ihw', pred, proto)  # (i, 32) @ (32, 160, 160) -> (i, 160, 160)
        """
        _, _, mask_h, mask_w = proto.shape
        loss = 0

        # Normalize to 0-1
        target_bboxes_normalized = target_bboxes / imgsz[[1, 0, 1, 0]]

        # Areas of target bboxes
        marea = xyxy2xywh(target_bboxes_normalized)[..., 2:].prod(2)

        # Normalize to mask size
        mxyxy = target_bboxes_normalized * torch.tensor([mask_w, mask_h, mask_w, mask_h], device=proto.device)

        for i, single_i in enumerate(zip(fg_mask, target_gt_idx, pred_masks, proto, mxyxy, marea, masks)):
            fg_mask_i, target_gt_idx_i, pred_masks_i, proto_i, mxyxy_i, marea_i, masks_i = single_i
            if fg_mask_i.any():
                mask_idx = target_gt_idx_i[fg_mask_i]
                if overlap:
                    gt_mask = masks_i == (mask_idx + 1).view(-1, 1, 1)
                    gt_mask = gt_mask.float()
                else:
                    gt_mask = masks[batch_idx.view(-1) == i][mask_idx]

                loss += self.single_mask_loss(
                    gt_mask, pred_masks_i[fg_mask_i], proto_i, mxyxy_i[fg_mask_i], marea_i[fg_mask_i]
                )

            # WARNING: lines below prevents Multi-GPU DDP 'unused gradient' PyTorch errors, do not remove
            else:
                loss += (proto * 0).sum() + (pred_masks * 0).sum()  # inf sums may lead to nan loss

        return loss / fg_mask.sum()

v8PoseLoss

\[\begin{cases} L_{\text{box}} &= \frac{1}{S} \sum_{i \in \mathcal{F}} w_i \Bigl[1 - \text{IoU}(\hat{b}_i, b_i)\Bigr] \\ L_{\text{dfl}} &= \frac{1}{S} \sum_{i \in \mathcal{F}} w_i \cdot \text{DFLoss}(p_i, t_i) \\ L_{\text{cls}} &= \frac{1}{S} \sum_{i} \text{BCE}(p^{cls}_i, q_i) \\ L_{\text{kpt}} &= \frac{1}{N \cdot K} \sum_{i=1}^{N} \lambda_i \sum_{k=1}^{K} m_{i,k} \left[1 - \exp\Bigl(-\frac{d_{i,k}}{8\,\sigma_k^2\,(A_i + \epsilon)}\Bigr)\right] \\ L_{\text{kobj}} &= \text{BCE_pose}\Bigl(p^{\text{kobj}}_{i,k}, m_{i,k}\Bigr) \\ \mathcal{L} &= N \cdot \Bigl[ \lambda_{\text{box}} L_{\text{box}} + \lambda_{\text{pose}} L_{\text{kpt}} + \lambda_{\text{kobj}} L_{\text{kobj}} + \lambda_{\text{cls}} L_{\text{cls}} + \lambda_{\text{dfl}} L_{\text{dfl}} \Bigr], \quad \lambda_{\text{box}} = \text{self.hyp.box} \end{cases}\]

class v8PoseLoss(v8DetectionLoss):
    """Criterion class for computing training losses."""

    def __init__(self, model):  # model must be de-paralleled
        """Initializes v8PoseLoss with model, sets keypoint variables and declares a keypoint loss instance."""
        super().__init__(model)
        self.kpt_shape = model.model[-1].kpt_shape
        self.bce_pose = nn.BCEWithLogitsLoss()
        is_pose = self.kpt_shape == [17, 3]
        nkpt = self.kpt_shape[0]  # number of keypoints
        sigmas = torch.from_numpy(OKS_SIGMA).to(self.device) if is_pose else torch.ones(nkpt, device=self.device) / nkpt
        self.keypoint_loss = KeypointLoss(sigmas=sigmas)

    def __call__(self, preds, batch):
        """Calculate the total loss and detach it."""
        loss = torch.zeros(5, device=self.device)  # box, cls, dfl, kpt_location, kpt_visibility
        feats, pred_kpts = preds if isinstance(preds[0], list) else preds[1]
        pred_distri, pred_scores = torch.cat([xi.view(feats[0].shape[0], self.no, -1) for xi in feats], 2).split(
            (self.reg_max * 4, self.nc), 1
        )

        # B, grids, ..
        pred_scores = pred_scores.permute(0, 2, 1).contiguous()
        pred_distri = pred_distri.permute(0, 2, 1).contiguous()
        pred_kpts = pred_kpts.permute(0, 2, 1).contiguous()

        dtype = pred_scores.dtype
        imgsz = torch.tensor(feats[0].shape[2:], device=self.device, dtype=dtype) * self.stride[0]  # image size (h,w)
        anchor_points, stride_tensor = make_anchors(feats, self.stride, 0.5)

        # Targets
        batch_size = pred_scores.shape[0]
        batch_idx = batch["batch_idx"].view(-1, 1)
        targets = torch.cat((batch_idx, batch["cls"].view(-1, 1), batch["bboxes"]), 1)
        targets = self.preprocess(targets.to(self.device), batch_size, scale_tensor=imgsz[[1, 0, 1, 0]])
        gt_labels, gt_bboxes = targets.split((1, 4), 2)  # cls, xyxy
        mask_gt = gt_bboxes.sum(2, keepdim=True).gt_(0.0)

        # Pboxes
        pred_bboxes = self.bbox_decode(anchor_points, pred_distri)  # xyxy, (b, h*w, 4)
        pred_kpts = self.kpts_decode(anchor_points, pred_kpts.view(batch_size, -1, *self.kpt_shape))  # (b, h*w, 17, 3)

        _, target_bboxes, target_scores, fg_mask, target_gt_idx = self.assigner(
            pred_scores.detach().sigmoid(),
            (pred_bboxes.detach() * stride_tensor).type(gt_bboxes.dtype),
            anchor_points * stride_tensor,
            gt_labels,
            gt_bboxes,
            mask_gt,
        )

        target_scores_sum = max(target_scores.sum(), 1)

        # Cls loss
        # loss[1] = self.varifocal_loss(pred_scores, target_scores, target_labels) / target_scores_sum  # VFL way
        loss[3] = self.bce(pred_scores, target_scores.to(dtype)).sum() / target_scores_sum  # BCE

        # Bbox loss
        if fg_mask.sum():
            target_bboxes /= stride_tensor
            loss[0], loss[4] = self.bbox_loss(
                pred_distri, pred_bboxes, anchor_points, target_bboxes, target_scores, target_scores_sum, fg_mask
            )
            keypoints = batch["keypoints"].to(self.device).float().clone()
            keypoints[..., 0] *= imgsz[1]
            keypoints[..., 1] *= imgsz[0]

            loss[1], loss[2] = self.calculate_keypoints_loss(
                fg_mask, target_gt_idx, keypoints, batch_idx, stride_tensor, target_bboxes, pred_kpts
            )

        loss[0] *= self.hyp.box  # box gain
        loss[1] *= self.hyp.pose  # pose gain
        loss[2] *= self.hyp.kobj  # kobj gain
        loss[3] *= self.hyp.cls  # cls gain
        loss[4] *= self.hyp.dfl  # dfl gain

        return loss.sum() * batch_size, loss.detach()  # loss(box, cls, dfl)

    @staticmethod
    def kpts_decode(anchor_points, pred_kpts):
        """Decodes predicted keypoints to image coordinates."""
        y = pred_kpts.clone()
        y[..., :2] *= 2.0
        y[..., 0] += anchor_points[:, [0]] - 0.5
        y[..., 1] += anchor_points[:, [1]] - 0.5
        return y

    def calculate_keypoints_loss(
        self, masks, target_gt_idx, keypoints, batch_idx, stride_tensor, target_bboxes, pred_kpts
    ):
        """
        Calculate the keypoints loss for the model.

        This function calculates the keypoints loss and keypoints object loss for a given batch. The keypoints loss is
        based on the difference between the predicted keypoints and ground truth keypoints. The keypoints object loss is
        a binary classification loss that classifies whether a keypoint is present or not.

        Args:
            masks (torch.Tensor): Binary mask tensor indicating object presence, shape (BS, N_anchors).
            target_gt_idx (torch.Tensor): Index tensor mapping anchors to ground truth objects, shape (BS, N_anchors).
            keypoints (torch.Tensor): Ground truth keypoints, shape (N_kpts_in_batch, N_kpts_per_object, kpts_dim).
            batch_idx (torch.Tensor): Batch index tensor for keypoints, shape (N_kpts_in_batch, 1).
            stride_tensor (torch.Tensor): Stride tensor for anchors, shape (N_anchors, 1).
            target_bboxes (torch.Tensor): Ground truth boxes in (x1, y1, x2, y2) format, shape (BS, N_anchors, 4).
            pred_kpts (torch.Tensor): Predicted keypoints, shape (BS, N_anchors, N_kpts_per_object, kpts_dim).

        Returns:
            kpts_loss (torch.Tensor): The keypoints loss.
            kpts_obj_loss (torch.Tensor): The keypoints object loss.
        """
        batch_idx = batch_idx.flatten()
        batch_size = len(masks)

        # Find the maximum number of keypoints in a single image
        max_kpts = torch.unique(batch_idx, return_counts=True)[1].max()

        # Create a tensor to hold batched keypoints
        batched_keypoints = torch.zeros(
            (batch_size, max_kpts, keypoints.shape[1], keypoints.shape[2]), device=keypoints.device
        )

        # TODO: any idea how to vectorize this?
        # Fill batched_keypoints with keypoints based on batch_idx
        for i in range(batch_size):
            keypoints_i = keypoints[batch_idx == i]
            batched_keypoints[i, : keypoints_i.shape[0]] = keypoints_i

        # Expand dimensions of target_gt_idx to match the shape of batched_keypoints
        target_gt_idx_expanded = target_gt_idx.unsqueeze(-1).unsqueeze(-1)

        # Use target_gt_idx_expanded to select keypoints from batched_keypoints
        selected_keypoints = batched_keypoints.gather(
            1, target_gt_idx_expanded.expand(-1, -1, keypoints.shape[1], keypoints.shape[2])
        )

        # Divide coordinates by stride
        selected_keypoints /= stride_tensor.view(1, -1, 1, 1)

        kpts_loss = 0
        kpts_obj_loss = 0

        if masks.any():
            gt_kpt = selected_keypoints[masks]
            area = xyxy2xywh(target_bboxes[masks])[:, 2:].prod(1, keepdim=True)
            pred_kpt = pred_kpts[masks]
            kpt_mask = gt_kpt[..., 2] != 0 if gt_kpt.shape[-1] == 3 else torch.full_like(gt_kpt[..., 0], True)
            kpts_loss = self.keypoint_loss(pred_kpt, gt_kpt, kpt_mask, area)  # pose loss

            if pred_kpt.shape[-1] == 3:
                kpts_obj_loss = self.bce_pose(pred_kpt[..., 2], kpt_mask.float())  # keypoint obj loss

        return kpts_loss, kpts_obj_loss

v8ClassificationLoss

\[L = -\sum y \log(p)\]

class v8ClassificationLoss:
    """Criterion class for computing training losses."""

    def __call__(self, preds, batch):
        """Compute the classification loss between predictions and true labels."""
        preds = preds[1] if isinstance(preds, (list, tuple)) else preds
        loss = F.cross_entropy(preds, batch["cls"], reduction="mean")
        loss_items = loss.detach()
        return loss, loss_items

v8OBBLoss

\[L = L_{box} + L_{cls} + L_{dfl}\]

class v8OBBLoss(v8DetectionLoss):
    """Calculates losses for object detection, classification, and box distribution in rotated YOLO models."""

    def __init__(self, model):
        """Initializes v8OBBLoss with model, assigner, and rotated bbox loss; note model must be de-paralleled."""
        super().__init__(model)
        self.assigner = RotatedTaskAlignedAssigner(topk=10, num_classes=self.nc, alpha=0.5, beta=6.0)
        self.bbox_loss = RotatedBboxLoss(self.reg_max).to(self.device)

    def preprocess(self, targets, batch_size, scale_tensor):
        """Preprocesses the target counts and matches with the input batch size to output a tensor."""
        if targets.shape[0] == 0:
            out = torch.zeros(batch_size, 0, 6, device=self.device)
        else:
            i = targets[:, 0]  # image index
            _, counts = i.unique(return_counts=True)
            counts = counts.to(dtype=torch.int32)
            out = torch.zeros(batch_size, counts.max(), 6, device=self.device)
            for j in range(batch_size):
                matches = i == j
                if n := matches.sum():
                    bboxes = targets[matches, 2:]
                    bboxes[..., :4].mul_(scale_tensor)
                    out[j, :n] = torch.cat([targets[matches, 1:2], bboxes], dim=-1)
        return out

    def __call__(self, preds, batch):
        """Calculate and return the loss for the YOLO model."""
        loss = torch.zeros(3, device=self.device)  # box, cls, dfl
        feats, pred_angle = preds if isinstance(preds[0], list) else preds[1]
        batch_size = pred_angle.shape[0]  # batch size, number of masks, mask height, mask width
        pred_distri, pred_scores = torch.cat([xi.view(feats[0].shape[0], self.no, -1) for xi in feats], 2).split(
            (self.reg_max * 4, self.nc), 1
        )

        # b, grids, ..
        pred_scores = pred_scores.permute(0, 2, 1).contiguous()
        pred_distri = pred_distri.permute(0, 2, 1).contiguous()
        pred_angle = pred_angle.permute(0, 2, 1).contiguous()

        dtype = pred_scores.dtype
        imgsz = torch.tensor(feats[0].shape[2:], device=self.device, dtype=dtype) * self.stride[0]  # image size (h,w)
        anchor_points, stride_tensor = make_anchors(feats, self.stride, 0.5)

        # targets
        try:
            batch_idx = batch["batch_idx"].view(-1, 1)
            targets = torch.cat((batch_idx, batch["cls"].view(-1, 1), batch["bboxes"].view(-1, 5)), 1)
            rw, rh = targets[:, 4] * imgsz[0].item(), targets[:, 5] * imgsz[1].item()
            targets = targets[(rw >= 2) & (rh >= 2)]  # filter rboxes of tiny size to stabilize training
            targets = self.preprocess(targets.to(self.device), batch_size, scale_tensor=imgsz[[1, 0, 1, 0]])
            gt_labels, gt_bboxes = targets.split((1, 5), 2)  # cls, xywhr
            mask_gt = gt_bboxes.sum(2, keepdim=True).gt_(0.0)
        except RuntimeError as e:
            raise TypeError(
                "ERROR ❌ OBB dataset incorrectly formatted or not a OBB dataset.\n"
                "This error can occur when incorrectly training a 'OBB' model on a 'detect' dataset, "
                "i.e. 'yolo train model=yolo11n-obb.pt data=dota8.yaml'.\nVerify your dataset is a "
                "correctly formatted 'OBB' dataset using 'data=dota8.yaml' "
                "as an example.\nSee https://docs.ultralytics.com/datasets/obb/ for help."
            ) from e

        # Pboxes
        pred_bboxes = self.bbox_decode(anchor_points, pred_distri, pred_angle)  # xyxy, (b, h*w, 4)

        bboxes_for_assigner = pred_bboxes.clone().detach()
        # Only the first four elements need to be scaled
        bboxes_for_assigner[..., :4] *= stride_tensor
        _, target_bboxes, target_scores, fg_mask, _ = self.assigner(
            pred_scores.detach().sigmoid(),
            bboxes_for_assigner.type(gt_bboxes.dtype),
            anchor_points * stride_tensor,
            gt_labels,
            gt_bboxes,
            mask_gt,
        )

        target_scores_sum = max(target_scores.sum(), 1)

        # Cls loss
        # loss[1] = self.varifocal_loss(pred_scores, target_scores, target_labels) / target_scores_sum  # VFL way
        loss[1] = self.bce(pred_scores, target_scores.to(dtype)).sum() / target_scores_sum  # BCE

        # Bbox loss
        if fg_mask.sum():
            target_bboxes[..., :4] /= stride_tensor
            loss[0], loss[2] = self.bbox_loss(
                pred_distri, pred_bboxes, anchor_points, target_bboxes, target_scores, target_scores_sum, fg_mask
            )
        else:
            loss[0] += (pred_angle * 0).sum()

        loss[0] *= self.hyp.box  # box gain
        loss[1] *= self.hyp.cls  # cls gain
        loss[2] *= self.hyp.dfl  # dfl gain

        return loss.sum() * batch_size, loss.detach()  # loss(box, cls, dfl)

    def bbox_decode(self, anchor_points, pred_dist, pred_angle):
        """
        Decode predicted object bounding box coordinates from anchor points and distribution.

        Args:
            anchor_points (torch.Tensor): Anchor points, (h*w, 2).
            pred_dist (torch.Tensor): Predicted rotated distance, (bs, h*w, 4).
            pred_angle (torch.Tensor): Predicted angle, (bs, h*w, 1).

        Returns:
            (torch.Tensor): Predicted rotated bounding boxes with angles, (bs, h*w, 5).
        """
        if self.use_dfl:
            b, a, c = pred_dist.shape  # batch, anchors, channels
            pred_dist = pred_dist.view(b, a, 4, c // 4).softmax(3).matmul(self.proj.type(pred_dist.dtype))
        return torch.cat((dist2rbox(pred_dist, pred_angle, anchor_points), pred_angle), dim=-1)

E2EDetectLoss

\[L = L_{one2many} + L_{one2one}\]

class E2EDetectLoss:
    """Criterion class for computing training losses."""

    def __init__(self, model):
        """Initialize E2EDetectLoss with one-to-many and one-to-one detection losses using the provided model."""
        self.one2many = v8DetectionLoss(model, tal_topk=10)
        self.one2one = v8DetectionLoss(model, tal_topk=1)

    def __call__(self, preds, batch):
        """Calculate the sum of the loss for box, cls and dfl multiplied by batch size."""
        preds = preds[1] if isinstance(preds, tuple) else preds
        one2many = preds["one2many"]
        loss_one2many = self.one2many(one2many, batch)
        one2one = preds["one2one"]
        loss_one2one = self.one2one(one2one, batch)
        return loss_one2many[0] + loss_one2one[0], loss_one2many[1] + loss_one2one[1]

NMS

def non_max_suppression(prediction, conf_thres=0.25, iou_thres=0.45, classes=None, agnostic=False, multi_label=False,
                        labels=(), max_det=300):
    """Runs Non-Maximum Suppression (NMS) on inference results

    Returns:
         list of detections, on (n,6) tensor per image [xyxy, conf, cls]
    """

    nc = prediction.shape[2] - 5  # number of classes
    xc = prediction[..., 4] > conf_thres  # candidates

    # Checks
    assert 0 <= conf_thres <= 1, f'Invalid Confidence threshold {conf_thres}, valid values are between 0.0 and 1.0'
    assert 0 <= iou_thres <= 1, f'Invalid IoU {iou_thres}, valid values are between 0.0 and 1.0'

    # Settings
    min_wh, max_wh = 2, 4096  # (pixels) minimum and maximum box width and height
    max_nms = 30000  # maximum number of boxes into torchvision.ops.nms()
    time_limit = 10.0  # seconds to quit after
    redundant = True  # require redundant detections
    multi_label &= nc > 1  # multiple labels per box (adds 0.5ms/img)
    merge = False  # use merge-NMS

    t = time.time()
    output = [torch.zeros((0, 6), device=prediction.device)] * prediction.shape[0]
    for xi, x in enumerate(prediction):  # image index, image inference
        # Apply constraints
        # x[((x[..., 2:4] < min_wh) | (x[..., 2:4] > max_wh)).any(1), 4] = 0  # width-height
        x = x[xc[xi]]  # confidence

        # Cat apriori labels if autolabelling
        if labels and len(labels[xi]):
            l = labels[xi]
            v = torch.zeros((len(l), nc + 5), device=x.device)
            v[:, :4] = l[:, 1:5]  # box
            v[:, 4] = 1.0  # conf
            v[range(len(l)), l[:, 0].long() + 5] = 1.0  # cls
            x = torch.cat((x, v), 0)

        # If none remain process next image
        if not x.shape[0]:
            continue

        # Compute conf
        x[:, 5:] *= x[:, 4:5]  # conf = obj_conf * cls_conf

        # Box (center x, center y, width, height) to (x1, y1, x2, y2)
        box = xywh2xyxy(x[:, :4])

        # Detections matrix nx6 (xyxy, conf, cls)
        if multi_label:
            i, j = (x[:, 5:] > conf_thres).nonzero(as_tuple=False).T
            x = torch.cat((box[i], x[i, j + 5, None], j[:, None].float()), 1)
        else:  # best class only
            conf, j = x[:, 5:].max(1, keepdim=True)
            x = torch.cat((box, conf, j.float()), 1)[conf.view(-1) > conf_thres]

        # Filter by class
        if classes is not None:
            x = x[(x[:, 5:6] == torch.tensor(classes, device=x.device)).any(1)]

        # Apply finite constraint
        # if not torch.isfinite(x).all():
        #     x = x[torch.isfinite(x).all(1)]

        # Check shape
        n = x.shape[0]  # number of boxes
        if not n:  # no boxes
            continue
        elif n > max_nms:  # excess boxes
            x = x[x[:, 4].argsort(descending=True)[:max_nms]]  # sort by confidence

        # Batched NMS
        c = x[:, 5:6] * (0 if agnostic else max_wh)  # classes
        boxes, scores = x[:, :4] + c, x[:, 4]  # boxes (offset by class), scores
        i = torchvision.ops.nms(boxes, scores, iou_thres)  # NMS
        if i.shape[0] > max_det:  # limit detections
            i = i[:max_det]
        if merge and (1 < n < 3E3):  # Merge NMS (boxes merged using weighted mean)
            # update boxes as boxes(i,4) = weights(i,n) * boxes(n,4)
            iou = box_iou(boxes[i], boxes) > iou_thres  # iou matrix
            weights = iou * scores[None]  # box weights
            x[i, :4] = torch.mm(weights, x[:, :4]).float() / weights.sum(1, keepdim=True)  # merged boxes
            if redundant:
                i = i[iou.sum(1) > 1]  # require redundancy

        output[xi] = x[i]
        if (time.time() - t) > time_limit:
            print(f'WARNING: NMS time limit {time_limit}s exceeded')
            break  # time limit exceeded

    return output

参考

1. Alpha-IoU: A Family of Power Intersection over Union Losses for Bounding Box Regression
2. Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression