Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

解决了什么问题

为了解决内部协变量偏移(Internal Covariate Shift)问题:
在网络的训练阶段，随着前几层的参数变化，输入到当前层的分布也相应变化，因此当前层需要不断调整以适应新的分布。这个问题对于深层网络来说尤其严重，因为较浅的隐藏层中的微小变化在网络内传播时会被放大，从而导致深层隐藏层的显著变化。因此，我们提出了批量标准化的方法来减少这些不必要的移位，从而加快训练速度并生成更可靠的模型。

优点

可以使用更高的学习率不用担心因此梯度消失或者爆炸
有正则化的效果,使网络有泛化特性不需要使用dropout来缓解过拟合
提升训练速度

缺点

mini-batch即m的值非常关键, 如果m值非常小,训练结果非常不稳定

方法

前向传播

\[y = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

反向传播

损失函数所有变量的偏导

\[\begin{align} \frac{\partial \ell}{\partial \hat x_{i}} &= \frac{\partial \ell}{\partial y_{i}} \gamma \\ \frac{\partial \ell}{\partial \sigma_{B}^{2}} &= \sum_{i=1}^{m}\frac{\partial \ell}{\partial \hat x_{i}}\frac{\partial \hat x_{i}}{\partial \sigma_{B}^{2}} = \sum_{i=1}^{m} \frac{\partial \ell}{\partial y_{i}} \gamma (x_{i} - \mu_{B})\frac{-1}{2}(\sigma_{B}^{2}+\epsilon )^{-\frac{3}{2} } \\ \frac{\partial \ell}{\partial \mu_{B}} &=\sum_{i = 1}^{m} \frac{\partial \ell}{\partial \hat x_{i}}\frac{\partial \hat x_{i}}{\mu_{B}} + \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{\partial \sigma_{B}^{2}}{\partial \mu_{B}} = \sum_{i = 1}^{m} \frac{\partial \ell}{\partial \hat x_{i}} \frac{-1}{\sqrt{\sigma_{B}^{2} + \epsilon } } + \sum_{i = 1}^{m} \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{-2}{m} (x_{i}-\mu_{B})\\ \frac{\partial \ell}{\partial x_{i}} &= \frac{\partial \ell}{\partial \hat x_{i}} \frac{\partial \hat x_{i}}{\partial x_{i}} + \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{\partial \sigma_{B}^{2}}{\partial x_{i}} + \frac{\partial \ell}{\partial \mu_{B}}\frac{\partial \mu_{B}}{\partial x_{i}} = \frac{\partial \ell}{\partial\hat x_{i}} \cdot \frac{1}{\sqrt{\sigma_{B}^{2} + \epsilon }} + \frac{\partial \ell}{\partial \sigma_{B}^{2}} \frac{2(x_{i} - \mu_{B})}{m} + \frac{\partial \ell}{\mu_{B}} \frac{1}{m}\\ \frac{\partial \ell}{\partial \gamma} &= \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}}\frac{\partial y_{i}}{\partial \gamma} = \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}} \hat {x_{i}}\\ \frac{\partial \ell}{\partial \beta} &= \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}}\frac{\partial y_{i}}{\partial \beta} = \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}}\\ \end{align}\]

根据链式法则:

分别计算,

\[\begin{align} \begin{cases} \frac{\partial \ell}{\partial \hat x_{i}} & = \frac{\partial \ell}{\partial y_{i}}\frac{\partial y_{i}}{\partial \hat x_{i}} = \frac{\partial \ell}{\partial y_{i}} \gamma \\ \frac{\partial \hat x_{i}}{\partial x_{i}} & = \frac{1}{\sqrt{\sigma_{B}^{2} + \epsilon }} \end{cases} \tag{1} \end{align}\] \[\begin{align} \begin{cases} \frac{\partial \ell}{\partial \sigma_{B}^{2}} & = \sum_{i=1}^{m}\frac{\partial \ell}{\partial \hat x_{i}}\frac{\partial \hat x_{i}}{\partial \sigma_{B}^{2}} = \sum_{i=1}^{m} \frac{\partial \ell}{\partial y_{i}} \gamma (x_{i} - \mu_{B})\frac{-1}{2}(\sigma_{B}^{2}+\epsilon )^{-\frac{3}{2} } \\ \frac{\partial \sigma_{B}^{2}}{\partial x_{i}} & = \sum_{i=1}^{m} \frac{2}{m} (x_{i} - \mu_{B}) \end{cases} \tag{2} \end{align}\] \[\begin{align} \begin{cases} \frac{\partial \ell}{\partial \mu_{B}} =\sum_{i = 1}^{m} \frac{\partial \ell}{\partial \hat x_{i}}\frac{\partial \hat x_{i}}{\mu_{B}} + \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{\partial \sigma_{B}^{2}}{\partial \mu_{B}} = \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}} \gamma \frac{-1}{\sqrt{\sigma_{B}^{2} + \epsilon } } + \sum_{i = 1}^{m} \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{-2}{m} (x_{i}-\mu_{B})\\ \frac{\partial \mu_{B}}{\partial x_{i}} = \frac{1}{m} \tag{3} \end{cases} \end{align}\]

把(1)(2)(3)式带入(0)可得,

\[\begin{align} \frac{\partial \ell}{\partial x_{i}} & = \frac{\partial \ell}{\partial \hat x_{i}} \frac{\partial \hat x_{i}}{\partial x_{i}} + \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{\partial \sigma_{B}^{2}}{\partial x_{i}} + \frac{\partial \ell}{\partial \mu_{B}}\frac{\partial \mu_{B}}{\partial x_{i}} \\ & = \frac{\partial \ell}{\partial y_{i}} \gamma \frac{1}{\sqrt{\sigma_{B}^{2} + \epsilon }} + \sum_{i=1}^{m} \frac{\partial \ell}{\partial y_{i}} \gamma (x_{i} - \mu_{B})\frac{-1}{2}(\sigma_{B}^{2}+\epsilon )^{-\frac{3}{2} }\frac{2}{m} (x_{i} - \mu_{B}) + \sum_{i = 1}^{m} (\frac{\partial \ell}{\partial y_{i}} \gamma \frac{-1}{\sqrt{\sigma_{B}^{2} + \epsilon } } + \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{-2}{m} (x_{i}-\mu_{B})) \frac{1}{m} \tag{4} \end{align}\] \[\begin{eqnarray} \frac{\partial \ell}{\partial \gamma} & = & \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}}\frac{\partial y_{i}}{\partial \gamma} = \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}} \hat {x_{i}}\tag{5} \end{eqnarray}\] \[\begin{eqnarray} \frac{\partial \ell}{\partial \beta} & = & \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}}\frac{\partial y_{i}}{\partial \beta} = \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}} \tag{6} \end{eqnarray}\]

训练BN网络

数据集

MNIST

效果

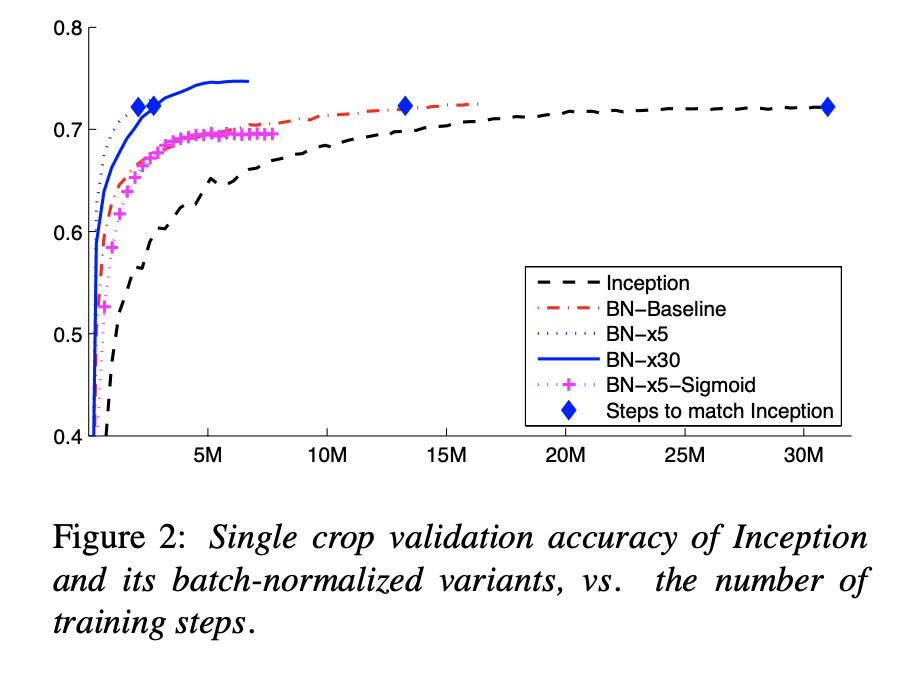
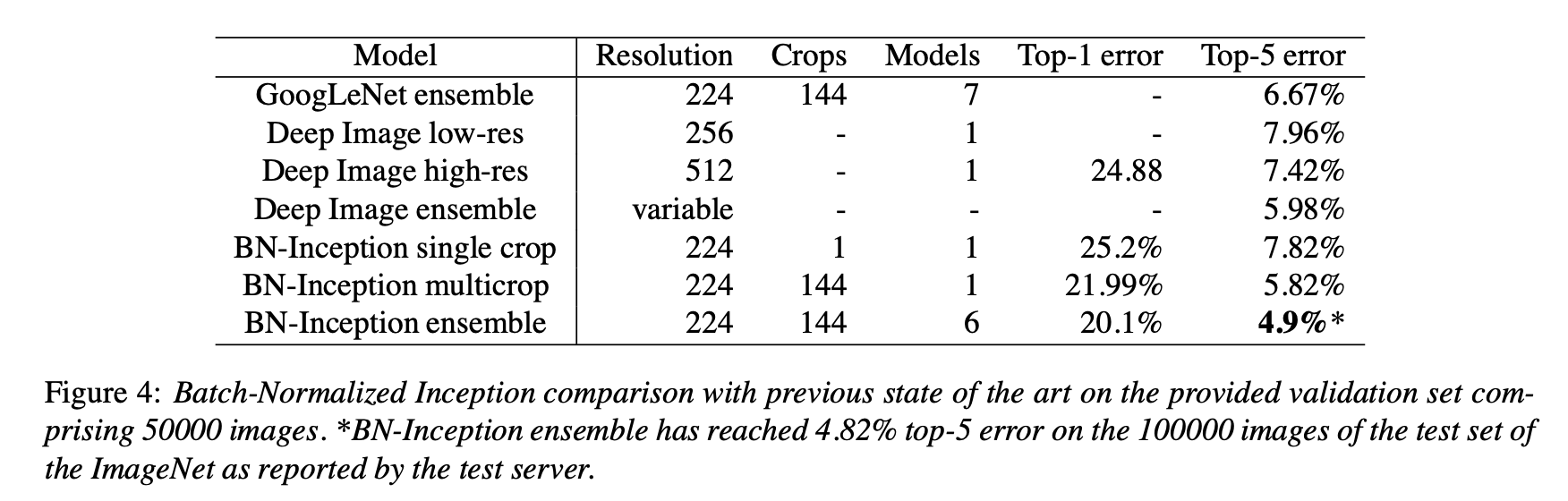
Code精读

Batch_Norm of Pytorch

The source of cpp

参数:


1.	batch	一个batch中包含的图片张数
2.	filters	该层神经网络的滤波器个数，即该层网络输出图片的通道数（比如对卷积网络来说，就是核的个数)
3.	spatial	该层神经网络每张输出特征图的尺寸，也即等于l.out_w*l.out_h
4.	m	batch * spatial
5.	biases	\(\beta\)
6.	scales	\(\gamma\)
7.	l.out_c	当前层的输出通道数
8.	l.delta	当前层累积误差

前向传播

void forward_batchnorm_layer(layer l, network net)
{
    if(l.type == BATCHNORM) copy_cpu(l.outputs*l.batch, net.input, 1, l.output, 1);
    copy_cpu(l.outputs*l.batch, l.output, 1, l.x, 1);
    if(net.train){
        mean_cpu(l.output, l.batch, l.out_c, l.out_h*l.out_w, l.mean);
        variance_cpu(l.output, l.mean, l.batch, l.out_c, l.out_h*l.out_w, l.variance);

        scal_cpu(l.out_c, .99, l.rolling_mean, 1);
        axpy_cpu(l.out_c, .01, l.mean, 1, l.rolling_mean, 1);
        scal_cpu(l.out_c, .99, l.rolling_variance, 1);
        axpy_cpu(l.out_c, .01, l.variance, 1, l.rolling_variance, 1);

        normalize_cpu(l.output, l.mean, l.variance, l.batch, l.out_c, l.out_h*l.out_w);   
        copy_cpu(l.outputs*l.batch, l.output, 1, l.x_norm, 1);
    } else {
        normalize_cpu(l.output, l.rolling_mean, l.rolling_variance, l.batch, l.out_c, l.out_h*l.out_w);
    }
    scale_bias(l.output, l.scales, l.batch, l.out_c, l.out_h*l.out_w);
    add_bias(l.output, l.biases, l.batch, l.out_c, l.out_h*l.out_w);
}

\(\mu_{B} = \frac{1}{m} \sum_{i=1}^{m} x_{i}^{2}\)

void mean_cpu(float *x, int batch, int filters, int spatial, float *mean)
{
    float scale = 1./(batch * spatial);
    int i,j,k;
    for(i = 0; i < filters; ++i){
        mean[i] = 0;
        for(j = 0; j < batch; ++j){
            for(k = 0; k < spatial; ++k){
                int index = j*filters*spatial + i*spatial + k;
                mean[i] += x[index];
            }
        }
        mean[i] *= scale;
    }
}

\(\sigma_{B}^{2} = \frac{1}{m-1} \sum_{i=1}^{m} (x_{i} - \mu_{B})^{2}\)

void variance_cpu(float *x, float *mean, int batch, int filters, int spatial, float *variance)
{
    float scale = 1./(batch * spatial - 1);
    int i,j,k;
    for(i = 0; i < filters; ++i){
        variance[i] = 0;
        for(j = 0; j < batch; ++j){
            for(k = 0; k < spatial; ++k){
                int index = j*filters*spatial + i*spatial + k;
                variance[i] += pow((x[index] - mean[i]), 2);
            }
        }
        variance[i] *= scale;
    }
}

移动平均值

\(\alpha\mu_{roll}+(1-\alpha)\mu\)

scal_cpu(l.out_c, .99, l.rolling_mean, 1);
axpy_cpu(l.out_c, .01, l.mean, 1, l.rolling_mean, 1);
void scal_cpu(int N, float ALPHA, float *X, int INCX)
{
    int i;
    for(i = 0; i < N; ++i) X[i*INCX] *= ALPHA;
}
void axpy_cpu(int N, float ALPHA, float *X, int INCX, float *Y, int INCY)
{
    int i;
    for(i = 0; i < N; ++i) Y[i*INCY] += ALPHA*X[i*INCX];
}

\(\hat x_{i} = \frac{x_{i} - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}}\)

void normalize_cpu(float *x, float *mean, float *variance, int batch, int filters, int spatial)
{
    int b, f, i;
    for(b = 0; b < batch; ++b){
        for(f = 0; f < filters; ++f){
            for(i = 0; i < spatial; ++i){
                int index = b*filters*spatial + f*spatial + i;
                x[index] = (x[index] - mean[f])/(sqrt(variance[f]) + .000001f);
            }
        }
    }
}

\(y_{i} = \gamma \hat x_{i} + \beta\)

void scale_bias(float *output, float *scales, int batch, int n, int size)
{
    int i,j,b;
    for(b = 0; b < batch; ++b){
        for(i = 0; i < n; ++i){
            for(j = 0; j < size; ++j){
                output[(b*n + i)*size + j] *= scales[i];
            }
        }
    }
}
void add_bias(float *output, float *biases, int batch, int n, int size)
{
    int i,j,b;
    for(b = 0; b < batch; ++b){
        for(i = 0; i < n; ++i){
            for(j = 0; j < size; ++j){
                output[(b*n + i)*size + j] += biases[i];
            }
        }
    }
}

反向传播

void backward_batchnorm_layer(layer l, network net)
{
    if(!net.train){
        l.mean = l.rolling_mean;
        l.variance = l.rolling_variance;
    }
    backward_bias(l.bias_updates, l.delta, l.batch, l.out_c, l.out_w*l.out_h);
    backward_scale_cpu(l.x_norm, l.delta, l.batch, l.out_c, l.out_w*l.out_h, l.scale_updates);

    scale_bias(l.delta, l.scales, l.batch, l.out_c, l.out_h*l.out_w);

    variance_delta_cpu(l.x, l.delta, l.mean, l.variance, l.batch, l.out_c, l.out_w*l.out_h, l.variance_delta);
    mean_delta_cpu(l.x, l.delta, l.variance, l.mean, l.batch, l.out_c, l.out_w*l.out_h, l.mean_delta, l.variance_delta);
    normalize_delta_cpu(l.x, l.mean, l.variance, l.mean_delta, l.variance_delta, l.batch, l.out_c, l.out_w*l.out_h, l.delta);
    if(l.type == BATCHNORM) copy_cpu(l.outputs*l.batch, l.delta, 1, net.delta, 1);
}

\(\frac{\partial \ell}{\partial \mu_{B}} =\sum_{i = 1}^{m} \frac{\partial \ell}{\partial \hat x_{i}}\frac{\partial \hat x_{i}}{\mu_{B}} + \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{\partial \sigma_{B}^{2}}{\partial \mu_{B}} = \sum_{i = 1}^{m} \frac{\partial \ell}{\partial \hat x_{i}} \frac{-1}{\sqrt{\sigma_{B}^{2} + \epsilon } } + \sum_{i = 1}^{m} \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{-2}{m} (x_{i}-\mu_{B})\)

void mean_delta_cpu(float *x, float *delta, float *variance, float *mean, int batch, int filters, int spatial, float *mean_delta, float *variance_delta)
{

    int i,j,k;
    for(i = 0; i < filters; ++i){
        int t1 = 0;
        int t2 = 0;
        for (j = 0; j < batch; ++j) {
            for (k = 0; k < spatial; ++k) {
                int index = j*filters*spatial + i*spatial + k;
                t1 += delta[index];
                t2 += (x[index] - mean[i]);
            }
        }
        mean_delta[i] = t1 * (-1./sqrtf(variance[i] + .00001f)) + variance_delta[i] * t2 * (-2.) * / (spatial * batch);

    }
}

\(\frac{\partial \ell}{\partial \sigma_{B}^{2}} = \sum_{i=1}^{m}\frac{\partial \ell}{\partial \hat x_{i}}\frac{\partial \hat x_{i}}{\partial \sigma_{B}^{2}} = \sum_{i=1}^{m} \frac{\partial \ell}{\partial y_{i}} \gamma (x_{i} - \mu_{B})\frac{-1}{2}(\sigma_{B}^{2}+\epsilon )^{-\frac{3}{2} }\)

void  variance_delta_cpu(float *x, float *delta, float *mean, float *variance, int batch, int filters, int spatial, float *variance_delta)
{

    int i,j,k;
    for(i = 0; i < filters; ++i){
        variance_delta[i] = 0;
        for(j = 0; j < batch; ++j){
            for(k = 0; k < spatial; ++k){
                int index = j*filters*spatial + i*spatial + k;
                variance_delta[i] += delta[index]*(x[index] - mean[i]);
            }
        }
        variance_delta[i] *= -.5 * powf(variance[i] + .00001f, (float)(-3./2.));
    }
}

\(\begin{align} \frac{\partial \ell}{\partial x_{i}} & = \frac{\partial \ell}{\partial \hat x_{i}} \frac{\partial \hat x_{i}}{\partial x_{i}} + \frac{\partial \ell}{\partial \sigma_{B}^{2}}\frac{\partial \sigma_{B}^{2}}{\partial x_{i}} + \frac{\partial \ell}{\partial \mu_{B}}\frac{\partial \mu_{B}}{\partial x_{i}} \\ & = \frac{\partial \ell}{\partial\hat x_{i}} \cdot \frac{1}{\sqrt{\sigma_{B}^{2} + \epsilon }} + \frac{\partial \ell}{\partial \sigma_{B}^{2}} \frac{2(x_{i} - \mu_{B})}{m} + \frac{\partial \ell}{\mu_{B}} \frac{1}{m} \tag{4} \end{align}\)

void normalize_delta_cpu(float *x, float *mean, float *variance, float *mean_delta, float *variance_delta, int batch, int filters, int spatial, float *delta)
{
    int f, j, k;
    for(j = 0; j < batch; ++j){
        for(f = 0; f < filters; ++f){
            for(k = 0; k < spatial; ++k){
                int index = j*filters*spatial + f*spatial + k;
                delta[index] = delta[index] * 1./(sqrtf(variance[f] + .00001f)) + variance_delta[f] * 2. * (x[index] - mean[f]) / (spatial * batch) + mean_delta[f]/(spatial*batch);
            }
        }
    }
}

\(\begin{eqnarray} \frac{\partial \ell}{\partial \gamma} & = & \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}}\frac{\partial y_{i}}{\partial \gamma} = \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}} \hat {x_{i}}\tag{5} \end{eqnarray}\)

void backward_scale_cpu(float *x_norm, float *delta, int batch, int n, int size, float *scale_updates)
{
    int i,b,f;
    for(f = 0; f < n; ++f){
        float sum = 0;
        for(b = 0; b < batch; ++b){
            for(i = 0; i < size; ++i){
                int index = i + size*(f + n*b);
                sum += delta[index] * x_norm[index];
            }
        }
        scale_updates[f] += sum;
    }
}

\(\begin{eqnarray} \frac{\partial \ell}{\partial \beta} & = & \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}}\frac{\partial y_{i}}{\partial \beta} = \sum_{i = 1}^{m} \frac{\partial \ell}{\partial y_{i}} \tag{6} \end{eqnarray}\)

void backward_bias(float *bias_updates, float *delta, int batch, int n, int size)
{
    int i,b,f;
    for(f = 0; f < n; ++f){
        float sum = 0;
        for(b = 0; b < batch; ++b){
            for(i = 0; i < size; ++i){
                int index = i + size*(f + n*b);
                sum += delta[index];
            }
        }
        scale_updates[f] += sum;
    }
}

解决了什么问题

优点

缺点

方法

前向传播

反向传播

训练BN网络

数据集

效果

Code精读

Batch_Norm of Pytorch

前向传播

反向传播

参考