Layer Normalization

Posted on | 0 comments
Words count in article 1818 | Reading time 9

Layer Normalization Loading...

解决了什么问题

旨在解决 Batch Normalization 在递归神经网络（RNN）等时间序列任务中表现不佳的缺陷。与 Batch Normalization 依赖 mini-batch 进行归一化不同，Layer Normalization 对每个样本的特征进行归一化，因此与 batch size 无关，特别适合处理单个样本的任务。

作者简介

Layer Normalization 论文的三位作者分别是 Jimmy Lei Ba、Jamie Ryan Kiros 和 Geoffrey E. Hinton，他们在深度学习领域都有重要的贡献。以下是对他们的介绍：

1. Jimmy Lei Ba

  • 背景: Jimmy Lei Ba 是一位知名的机器学习研究员，尤其在深度学习领域贡献显著。他曾在 Geoffrey Hinton 的指导下完成博士学位，主要研究领域涉及神经网络的优化、归一化技术、强化学习和深度学习模型的训练方法。
  • 贡献:
    • Layer Normalization 是他的一项重要贡献，解决了 Batch Normalization 在序列建模任务中的局限性。
    • 他还参与了多个与强化学习和神经网络结构相关的研究，发表了大量有影响力的论文。
  • 当前工作: Jimmy Lei Ba 目前是多伦多大学的助理教授，同时与 Google Brain 和其他领先的 AI 实验室有密切的合作。

2. Jamie Ryan Kiros

  • 背景: Jamie Ryan Kiros 是一名活跃的深度学习研究员，曾在多伦多大学深造，并与 Geoffrey Hinton 等顶尖学者合作。他的研究方向涵盖自然语言处理（NLP）、图像-文本联合学习以及深度神经网络的优化技术。
  • 贡献:
    • Kiros 是多个与文本生成、语言模型以及深度学习框架相关的重要研究的作者，尤其在语言-视觉学习（如文本和图像的联合表示学习）领域表现突出。
    • 他的工作涉及如何通过深度学习构建更好的表征模型，尤其是在多模态和语言任务中。
  • 当前工作: 他曾在 Google Brain 参与自然语言处理项目，并在业界和学术界有广泛影响力。

3. Geoffrey E. Hinton

  • 背景: Geoffrey Hinton 是深度学习领域的奠基者之一，被誉为“深度学习之父”。他是多伦多大学的教授，也是 Google Brain 的杰出研究员。他的研究涉及神经网络、深度学习、认知科学、强化学习等多个领域。
  • 贡献:
    • 反向传播算法: Hinton 是反向传播算法的发明者之一，该算法是深度神经网络训练的核心技术。
    • 深度学习复兴: 在 2012 年，他与学生 Alex Krizhevsky 和 Ilya Sutskever 一起通过 AlexNet 在 ImageNet 大赛上的突破性表现，推动了深度学习的广泛应用。
    • 他还提出了受限玻尔兹曼机（RBM）和深度置信网络（DBN），并为现代卷积神经网络和强化学习等领域提供了基础理论。
    • Turing 奖得主: 由于对人工智能领域的巨大贡献，Hinton 与 Yoshua Bengio 和 Yann LeCun 一起在 2018 年获得了图灵奖，这是计算机科学领域的最高荣誉。
  • 当前工作: 他在 Google Brain 和多伦多大学继续从事前沿的人工智能研究。

这三位作者的共同点是他们都在深度学习、神经网络和自然语言处理等领域有着深厚的研究背景，特别是 Geoffrey Hinton 在推动深度学习复兴方面具有里程碑式的贡献。Jimmy Lei Ba 和 Jamie Ryan Kiros 都是 Hinton 的学生，并在他的指导下做出了创新性工作，如 Layer Normalization。

优点

  1. 解决小批量问题：Layer Normalization 通过对每个单独样本的所有特征进行归一化，解决了 Batch Normalization 对 mini-batch 大小的依赖，尤其在 batch size 较小或 RNN 中表现出色。

  2. 适用于递归网络：Layer Normalization 不依赖于 batch size，因此更适合递归神经网络（RNN）或 Transformer 等结构，在自然语言处理和序列建模任务中具有优势。

  3. 与 Batch Normalization 的比较：该论文系统性地对比了 Layer Normalization 和 Batch Normalization 的效果，展示了在多种任务中的表现，尤其在语言建模等序列任务中的优势。

缺点

  1. 训练加速效果不如 BN：在像 CNN 这种依赖较大 batch size 的模型中，LN 可能无法像 BN 那样显著加速训练，尤其是在计算较高维度时。

  2. 正则化效果较弱：由于 LN 不依赖 mini-batch，无法像 BN 那样在大 batch size 时起到额外的正则化效果。

与Batch Normalization对比

特性 Batch Normalization (BN) Layer Normalization (LN)
归一化方式 基于 mini-batch 的均值和方差 基于单个样本内的均值和方差
对 batch size 的依赖 依赖 batch size，大 batch size 表现更好 不依赖 batch size，小 batch size 也有效
应用场景 CNN、MLP 等静态模型，深层网络 RNN、Transformer 等序列模型
训练加速 提供较好的训练加速效果 加速效果不如 BN
推理一致性 训练和推理时归一化方式不同，需做额外处理 训练和推理时一致
正则化效果 较好，依赖 mini-batch 较弱

方法

下面通过表格比较 Layer Normalization (LN) 和 Batch Normalization (BN) 的伪代码，展示它们的主要操作差异。

步骤 Layer Normalization (LN) 伪代码 Batch Normalization (BN) 伪代码
输入 - 输入特征 \(( x \in \mathbb{R}^{d} )\)（每个样本维度为 \(( d )\)） - 输入特征 \(( x \in \mathbb{R}^{m \times d} )\)（batch size 为 \(( m )\)，维度为 \(( d )\)）
1. 计算均值 - 对每个样本的特征维度计算均值：
\(( \mu = \frac{1}{d} \sum_{i=1}^{d} x_i )\)		 - 对 mini-batch 计算每一维特征的均值：
\(( \mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i )\)
2. 计算方差 - 对每个样本的特征维度计算方差：
\(( \sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2 )\)		 - 对 mini-batch 计算每一维特征的方差：
\(( \sigma_B^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2 )\)
3. 标准化 - 将每个特征标准化：
\(( \hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}} )\)		 - 将 mini-batch 中每个特征标准化：
\(( \hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} )\)
4. 缩放和平移 - 应用可学习参数对标准化后的输出进行缩放和平移：
\(( y_i = \gamma \hat{x}_i + \beta )\)		 - 应用可学习参数对标准化后的输出进行缩放和平移：
\(( y_i = \gamma \hat{x}_i + \beta )\)
输出 - 输出归一化后的特征：\(( y \in \mathbb{R}^d )\) - 输出归一化后的特征：\(( y \in \mathbb{R}^{m \times d} )\)

数据集

1. Microsoft COCO (MSCOCO)

  • 任务：图像-文本嵌入、图像和文本检索
  • 描述：MSCOCO 是一个大规模的图像和文本数据集，包含带有详细描述的图片，广泛用于图像分类、物体检测、多模态学习等任务。
  • 下载链接：MSCOCO Dataset

2. CNN Corpus

  • 任务：阅读理解、问答任务
  • 描述：CNN Corpus 是一个由新闻文章和问题组成的数据集，常用于问答和阅读理解模型的训练与评估。
  • 下载链接：CNN/Daily Mail Dataset（可以在此页面找到 CNN corpus 以及相关数据）

3. BookCorpus

  • 任务：无监督句子表示学习
  • 描述：BookCorpus 包含从小说和书籍中提取的超过 1 亿字的文本，主要用于预训练语言模型和文本嵌入任务。
  • 下载链接：BookCorpus Dataset

4. SICK (Sentences Involving Compositional Knowledge)

  • 任务：语义相关性、文本蕴涵
  • 描述：SICK 数据集包含句子的语义相似性和蕴涵标注，广泛用于自然语言处理任务中的句子对相关性评估。
  • 下载链接：SICK Dataset

5. MNIST

  • 任务：手写数字识别、生成模型
  • 描述：MNIST 是一个用于手写数字识别的经典数据集，包含 7 万张 28x28 像素的灰度手写数字图像，广泛用于机器学习和计算机视觉任务。
  • 下载链接：MNIST Dataset

6. IAM-OnDB (IAM Online Handwriting Database)

  • 任务：手写序列生成
  • 描述：IAM-OnDB 包含手写文本的在线笔迹数据，包括每个字符的 x 和 y 坐标，广泛用于手写字符识别和生成任务。
  • 下载链接：IAM Handwriting Database

效果

Loading... Loading... Loading... Loading... Loading... Loading...

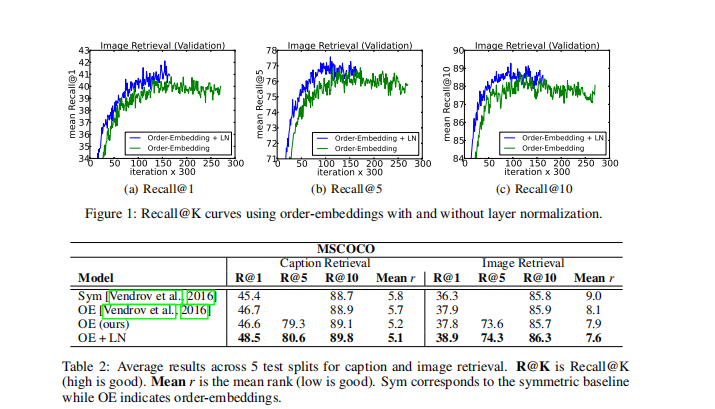
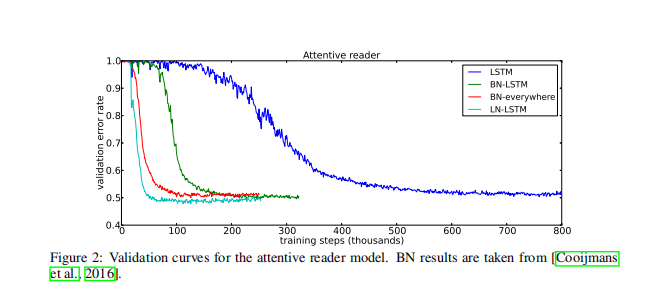
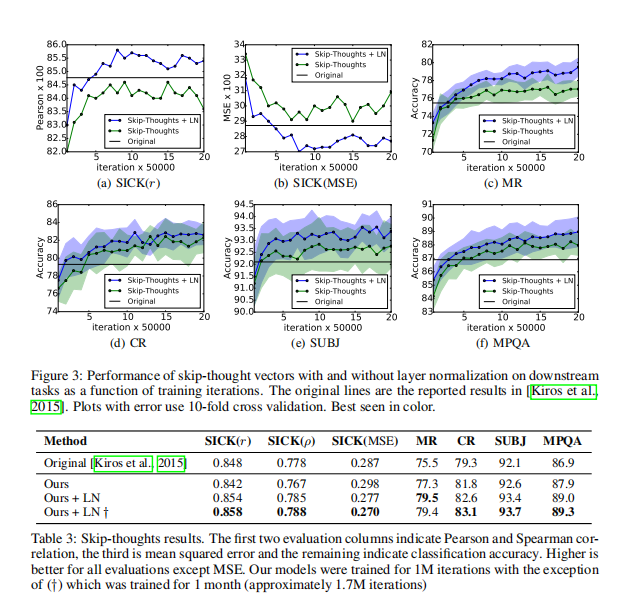
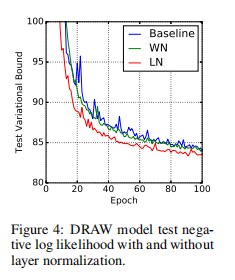
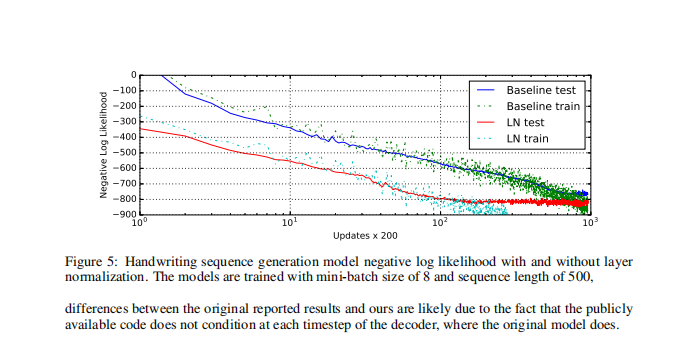
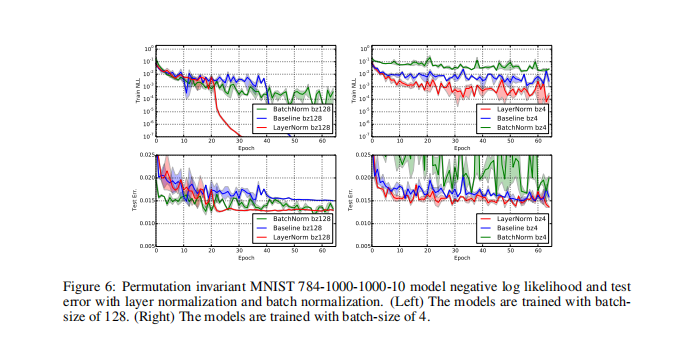
Code精读

The source of cpp

1. 计算均值

在 layer_norm_cpu 函数中，均值的计算通过 mean 进行处理：

auto M_N = _check_layer_norm_inputs(input, normalized_shape, weight, bias);
auto M = M_N.first;
auto N = M_N.second;
...
Tensor mean = at::empty({M}, X->options().dtype(dtype));

公式：

\[\mu = \frac{1}{N} \sum_{i=1}^{N} x_i\]

这里，mean 用于存储输入的均值。

2. 计算方差（标准差的倒数）

在 layer_norm_with_mean_rstd_out 函数中，方差和其倒数的计算是通过 LayerNormKernel 完成的：

LayerNormKernel(kCPU, input, gamma, beta, M, N, eps, &out, &mean, &rstd);

在 LayerNormKernel 的实现中，会计算方差 \(\sigma^2\) 和标准差的倒数：

const auto invstd = at::rsqrt(var + eps);

公式：

\(\sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2\) \(\hat{\sigma} = \frac{1}{\sqrt{\sigma^2 + \epsilon}}\)

这里，rstd 用于存储标准差的倒数。

3. 标准化

标准化操作在 LayerNormKernel 内部进行，其中的实现部分：

Y_ptr[j] = (X_ptr[j] + bias) * rstd_val;

公式：

\[\hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}\]

这里，Y_ptr[j] 存储了归一化后的输出。

4. 仿射变换（缩放和平移）

在 layer_norm_cpu 函数中，应用缩放和平移的部分如下：

if (weight.defined() && bias.defined()) {
    out = bias.addcmul(out, weight, 1);
} else if (weight.defined()) {
    out = out.mul(weight);
} else if (bias.defined()) {
    out = out.add(bias);
}

公式：

\[y_i = \gamma \cdot \hat{x}_i + \beta\]

这里，out 是归一化后的输出，weight 和 bias 分别对应于可学习参数 \(\gamma\) 和 \(\beta\)。

5. 反向传播

The source of cpp

在反向传播函数 layer_norm_backward_cpu 中，更新梯度的操作涉及的部分为：

LayerNormBackwardKernel(kCPU, dY, *X, mean, rstd, *gamma, M, N, &dX, &dgamma, &dbeta);

反向传播涉及的公式可以与前向传播的相反：

\[\frac{\partial L}{\partial x_i}, \quad \frac{\partial L}{\partial \gamma}, \quad \frac{\partial L}{\partial \beta}\]

其中 \(L\) 是损失函数，反向传播计算梯度用于更新模型的参数。 在 PyTorch 源代码中，LayerNormBackwardKernel 函数通常会定义在 layer_norm.cpp 或者其他与 Layer Normalization 相关的实现文件中。这个函数主要负责计算 Layer Normalization 的反向传播。

1. LayerNormBackwardKernel 的定义

LayerNormBackwardKernel 是通过 REGISTER_DISPATCH 宏注册的，因此它在后续代码中会被具体实现并调用。它的实现通常涉及到输入的梯度、均值、标准差和可学习参数的梯度计算。

REGISTER_DISPATCH(LayerNormBackwardKernel, &LayerNormBackwardKernelImpl);

2. LayerNormBackwardKernelImpl 的代码

具体的实现位于 LayerNormBackwardKernelImpl 中。这个实现会用到之前的 layer_norm_backward_frame 函数。以下是代码中的关键部分和它们所对应的公式。

计算梯度的主要部分
void LayerNormBackwardKernelImpl(
    const Tensor& dY,
    const Tensor& X,
    const Tensor& mean,
    const Tensor& rstd,
    const Tensor& gamma,
    int64_t M,
    int64_t N,
    Tensor* dX,
    Tensor* dgamma,
    Tensor* dbeta) {
  ...
  layer_norm_backward_frame<T, T2, opmath_t>(dY_data, X_data, mean_data, rstd_data, gamma_data, dX_data, dgamma_buffer_ptr, dbeta_buffer_ptr, scale, gamma_null, dX_null, dgamma_null, dbeta_null, N, i);
}

3. 公式对应

计算对 \(\gamma\) 的梯度

在 layer_norm_backward_frame 中，计算对权重 \(\gamma\) 的梯度的部分如下：

if (!dgamma_null) {
    const opmath_t a = rstd_data[i];
    const opmath_t b = -a * mean_data[i];
    vec::map3<T>(
        [a, b](Vec dgamma, Vec dy, Vec x) {
            return dgamma + dy * (Vec(a) * x + Vec(b));
        },
        dgamma_buffer_ptr,
        dY_ptr,
        X_ptr,
        N);
}

对应公式：

\[\frac{\partial L}{\partial \gamma} = \sum_i \frac{\partial L}{\partial y_i} \cdot \hat{x}_i\]

dy 是输出的梯度，x 是输入，计算后得到对 \(\gamma\) 的梯度。

计算对输入 \(x\) 的梯度

对输入的梯度 \(\frac{\partial L}{\partial x}\) 的计算如下：

if (!dX_null) {
    T* dX_ptr = dX_data + i * N;
    ...
    vec::map2<T>(
        [a, b, c](Vec dy, Vec x) {
            return Vec(a) * dy + Vec(b) * x + Vec(c);
        },
        dX_ptr,
        dY_ptr,
        X_ptr,
        N);
}

对应公式：

\[\frac{\partial L}{\partial x_i} = \frac{1}{\sqrt{\sigma^2 + \epsilon}} \left( \frac{\partial L}{\partial \hat{x}_i} - \frac{\sum_j \frac{\partial L}{\partial \hat{x}_j}}{N} - \hat{x}_i \frac{\sum_j \frac{\partial L}{\partial \hat{x}_j} \hat{x}_j}{N} \right)\]

dy 是输出的梯度，x 是输入，计算后得到对输入 \(x\) 的梯度。

计算对偏置 \(\beta\) 的梯度

计算对偏置 \(\beta\) 的梯度的部分如下：

if (!dbeta_null) {
    vec::map2<T>(
        [](Vec dbeta, Vec dy) { return dbeta + dy; },
        dbeta_buffer_ptr,
        dbeta_buffer_ptr,
        dY_ptr,
        N);
}

对应公式：

\[\frac{\partial L}{\partial \beta} = \sum_i \frac{\partial L}{\partial y_i}\]

dy 是输出的梯度。

代码中体现公式的部分总结

数学公式 代码片段 描述
\(\frac{\partial L}{\partial \gamma}\) vec::map3<T>(...); 计算对 \(\gamma\) 的梯度
\(\frac{\partial L}{\partial x_i}\) vec::map2<T>(...); 计算输入的梯度 \(\frac{\partial L}{\partial x_i}\)
\(\frac{\partial L}{\partial \beta}\) vec::map2<T>(...); 计算对 \(\beta\) 的梯度

总结

以下是上述代码中体现公式的关键部分：

公式 代码片段 描述
\(\mu = \frac{1}{N} \sum x_i\) Tensor mean = at::empty({M}, X->options().dtype(dtype)); 初始化均值张量。
\(\sigma^2 = \frac{1}{N} \sum (x_i - \mu)^2\) const auto invstd = at::rsqrt(var + eps); 计算标准差的倒数。
\(\hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}\) Y_ptr[j] = (X_ptr[j] + bias) * rstd_val; 对输入进行标准化处理。
\(y_i = \gamma \cdot \hat{x}_i + \beta\) out = bias.addcmul(out, weight, 1); 应用可学习参数进行仿射变换。
\(\frac{\partial L}{\partial x_i}\) LayerNormBackwardKernel(...) 计算反向传播的梯度更新。

参考

  1. Implementation of the paper: Layer Normalization
  2. The implementation of LN by Pytorch
  3. The source code for Layer Normalization in PyTorch (C++)